Difference between revisions of "B-Spline Automatic Registration"
(→Output files) |
m (→Normalized mutual information measure) |
||
| (44 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | This chapter describes the B-spline based registration of images in three dimensions (3D). The description specializes to two dimensions (2D) is in the obvious manner. | |
| − | + | Chapter is continued on the following pages: | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | *[[B-Spline Automatic Registration | B-Spline Automatic Registration - you are here]] | |
| − | + | *[[BSpline registration: Detecting folding]] | |
| − | + | *[[Examples of BSpline registration]] | |
| − | + | *[[User Dialogs in MIPAV | B-Spline Automatic Registration Dialog]] | |
| − | + | == Class implementation for MIPAV == | |
| + | |||
| + | The following classes are part of the <span style="font-family:courier">mipav/model/structures</span> package: | ||
| + | |||
| + | * B-splineBasis | ||
| + | * B-splineBasisDiscretef | ||
| + | * BSplineLattice2Df | ||
| + | * BSplineLattice3Df | ||
| + | * BSplineRegistrationBasef | ||
| + | * fBSplineRegistration2Df | ||
| + | |||
| + | The following classes are also part of the <span style="font-family:courier">mipav/model/algorithms</span>/registration package: | ||
| + | |||
| + | * AlgorithmRegBSpline | ||
| + | * AlgorithmRegBSpline2D | ||
| + | * AlgorithmRegBSpline3D | ||
| + | * AlgorithmRegBSpline25D | ||
| + | |||
| + | == Background == | ||
| + | |||
| + | <div id="Equation1"></div> | ||
| + | Let the target image have dimensions | ||
| + | <math> | ||
| + | (p_o)\,(p_o)\,(p_o) | ||
| + | </math> with image indices satisfying | ||
| + | <math> | ||
| + | 0\le j_0<p_0 | ||
| + | </math>, | ||
| + | <math> | ||
| + | 0\le j_1<p_1 | ||
| + | </math>, and | ||
| + | <math> | ||
| + | 0\le j_2<p_2 | ||
| + | </math>. Let the source image have dimensions <math> | ||
| + | (q_o)\,(q_o)\,(q_o) | ||
| + | </math> with image indices satisfying <math> | ||
| + | 0\le k_0<q_0 | ||
| + | </math>, <math> | ||
| + | 0\le k_1<q_1 | ||
| + | </math>, and <math> | ||
| + | 0\le k_2<q_2 | ||
| + | </math>. The B-spline volume function maps indices <math> | ||
| + | j_0,j_1,j_2 | ||
| + | </math> via equation 1. | ||
| + | |||
| + | Equation 1 <div align="left"><math> | ||
| + | M_{j_0, j_1, j_2} = \sum_{i_0=0}^{n_o} \left( N_{i_0},d_0,\frac{j_0}{p_0-1} \sum_{i_1=0}^{n_1} \left( N_{i_1}, \frac{j_1}{p_1-1} \sum_{i_2=0}^{n_2} N_{i_2}, d_2, \frac{j_2}{p_2-1}, B_{i_0, i_1, i_2} \right) \right) | ||
| + | |||
| + | |||
| + | </math></div><br /> | ||
| + | |||
| + | where the <math> | ||
| + | N_{i_e, d_e}(u) | ||
| + | </math> functions are the B-spline basis functions, and the ''B'' values are the control points. The numbers <math> | ||
| + | n_0,n_1,</math> and <math> n_2 </math>, are user selectable, the degrees | ||
| + | <math> | ||
| + | d_0,d_1,</math> and <math> d_2 | ||
| + | </math> for the basis functions are user selectable, and the B-spline basis functions are open and uniform. | ||
The control points have the following characteristics: | The control points have the following characteristics: | ||
* Each control point has coordinates from the unit cube. In two dimensions, each control point has coordinates from the unit square. | * Each control point has coordinates from the unit cube. In two dimensions, each control point has coordinates from the unit square. | ||
| − | * The initial placement of the control points depends on the B-spline basis and must yield the identity function; that is, | + | * The initial placement of the control points depends on the B-spline basis and must yield the identity function; that is, |
| + | <math> | ||
| + | M_{j_0j_1j_2} = (\frac {j_0} {p_0-1}), (\frac{j_1} {p_1-1}), (\frac {J_2)} {P_2+1}) | ||
| + | </math>. The initial placement of the control points is described in Section "Improving performance". | ||
* A control point is said to be in the outer layer if one of its indexes is either the minimum index (zero) or the maximum index (one less than the number of control points in a given dimension). The position of the control points in the outer layer are fixed as follows: | * A control point is said to be in the outer layer if one of its indexes is either the minimum index (zero) or the maximum index (one less than the number of control points in a given dimension). The position of the control points in the outer layer are fixed as follows: | ||
| − | Equation 2 <div align="left"> | + | Equation 2 <div align="left"><math> |
| + | B_0,i_1,i_2 =(0,y_{i_1},z_{i_2}) | ||
| + | </math> | ||
| − | + | <math> | |
| + | B_{i_0}, 0, i_2 = (\chi_{i_0}, 0, z_{i_2}) | ||
| + | </math> | ||
| − | + | <math> | |
| + | B_{i_0}, i_0, 0 = (\chi_{i_0}, y_{i_1}, 0) | ||
| + | </math> | ||
| − | + | <math> | |
| + | B_{n_0-1}, i_1, i_2 = (1, y_{i_1}, z_{i_2}) | ||
| + | </math> | ||
| − | + | <math> | |
| + | B_{i_0},n_1-1, i_2 = (\chi_{i_0}, 1, z_{i_2}) | ||
| + | </math> | ||
| − | + | <math> | |
| + | B_{i_0},i_1, n_2-1 = (\chi_{i_0}, y_{i_1}, 1) | ||
| + | </math> | ||
| + | |||
| + | </div><br /> | ||
| + | |||
| + | ; ''This constraint implies that the <math> | ||
| + | 0\le k^\prime_w<q_w | ||
| + | </math>'''' ''''for all w.'' | ||
| + | |||
| + | * A control point not in the outer layer is said to be an interior control point. The position of the interior control points is constrained such that its movement must not cause any folding in the B-spline transformation. ''Folding'' is defined to occur when there is a negative value anywhere in the computed deformation for the current B-spline transformation. The computation of the deformation is described in Section "Deformation". The method by which folding is detected is described in Section "Detect folding". | ||
| + | |||
| + | Each <math> | ||
| + | M_(j_0)(j_1)(j_2) | ||
| + | </math> contains normalized 3D coordinates (i.e., in the unit cube) that identify a location in the source image corresponding to the sample at <math> | ||
| + | (j_0,j_1,j_2) | ||
| + | </math> in the target image. The <math> | ||
| + | M_(j_0)(j_1)(j_2) | ||
| + | </math> coordinates are ''related to sample ''coordinates in the source image by <math> | ||
| + | M_{j_{0}, j_{1}, j_{2}} =\left( \frac {k^\prime_0}{q_0-1}, \frac{k^\prime_1}{q_1-1}, \frac{k^\prime_2}{q_2-1}\right) | ||
| + | </math> where the output indices <math> | ||
| + | k^\prime_0, k^\prime_1, k^\prime_2 | ||
| + | </math> are considered to be continuous values; that is, they are not necessarily integer valued. If the source image's samples are <math> | ||
| + | s_k\_0,k_1,k_2 | ||
| + | </math>, where <math> | ||
| + | 0\le k^\prime_w < q_w | ||
| + | </math> for all ''w'' , we need to evaluate the image at the nonintegral values <math> | ||
| + | k^\prime_0, k^\prime_1, k^\prime_2 | ||
| + | </math>. We can use trilinear interpolation to do this (use bilinear interpolation in the case of two-dimensional (2D) registration). Let <math> | ||
| + | k_w= |k^\prime_w| | ||
| + | </math>, the largest integer smaller than <math> k^\prime_w </math>. Define <math> | ||
| + | \Delta w = k^\prime_w - k_w | ||
| + | </math>. The interpolated image value is: | ||
| + | |||
| + | Equation 3 <br /> | ||
| + | <math> | ||
| + | U_0 = (1-\Delta_0)(S_{k_0,k_1,k_2}) + (\Delta_0)(S_{k_0 + 1,k_1,k_2}) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | U_1 = (1-\Delta_0)(S_{k_0,k_1+1,k_2} + (\Delta_0)(S_{k_0,k_1 + 1,k_2}) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | U_2 = (1-\Delta_0)(S_{k_0,k_1,k_2+1} + (\Delta_0)(S_{k_0+1,k_1,k_2+1}) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | U_3 = (1-\Delta_0)(S_{k_0,k_1+1,k_2+1} + (\Delta_0)(S_{k_0+1,k_1+1,k_2+1}) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \nu_0 = (1 - \Delta_1)U_0 + (\Delta_1)(U_1) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \nu_1 = (1 - \Delta_1)U_2 + (\Delta_1)(U_3) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | S(\kappa_0, \kappa_1, \kappa_2) = (1- \Delta_2)\nu_0 + (\Delta_2)(\nu_1) | ||
| + | </math> | ||
| + | |||
| + | If the target image samples are <math> | ||
| + | T_{j_0, j_1, j_2} | ||
| + | </math>, where <math> | ||
| + | 0 \le j_w < p_w | ||
| + | </math> for all ''w'', then the source image S is trilinearly interpolated at <math> | ||
| + | (k^\prime_0,k^\prime_1, k^\prime_2) | ||
| + | </math>, which are the coordinates of <math> | ||
| + | M_(j_0)(j_1)(j_2) | ||
| + | </math>. This means that the currently registered source image, denoted [[Image:BSplineRegistrationOV_withMath57.jpg]], has the same dimensions as the target image and can be defined in terms of the target image samples as <math> | ||
| + | S^\prime(j_0,j_1,j_2) = S(k^\prime_0,k^\prime_1, k^\prime_2) | ||
| + | </math>. A measure of error between the two images S''j0,j1,j2'' and T''j0,j1 ,j2 ''can be computed. A number of possible error measure functions are defined in Section 1.2. The goal is to select the control point positions to make the error measure as small as possible. This is done by moving a single control point at a time using gradient descent. | ||
The gradient of the error function is estimated for the control point Bi''0'',i''1'',i''2 ''by means of finite differences, where changes in the error function are measured for small steps of the control point from its current position in each of the coordinate axis directions. Let [[Image:BSplineRegistrationOV_withMath59.jpg]], [[Image:BSplineRegistrationOV_withMath60.jpg]]and [[Image:BSplineRegistrationOV_withMath61.jpg]] be small step sizes equivalent to one sample increment in the target image, | The gradient of the error function is estimated for the control point Bi''0'',i''1'',i''2 ''by means of finite differences, where changes in the error function are measured for small steps of the control point from its current position in each of the coordinate axis directions. Let [[Image:BSplineRegistrationOV_withMath59.jpg]], [[Image:BSplineRegistrationOV_withMath60.jpg]]and [[Image:BSplineRegistrationOV_withMath61.jpg]] be small step sizes equivalent to one sample increment in the target image, | ||
| − | Equation 4 <div align="left"> | + | Equation 4 <div align="left"><math> |
| + | \left( \Delta x = \frac{1} {p_0} \right),\left( \Delta y = \frac{1} {p_1} \right),\left( \Delta z = \frac{1} {p_2} \right) | ||
| + | </math></div><br /> | ||
The gradient of the error function is estimated at each control point B''i0,i1,i2''. The gradient at each control point is denoted by | The gradient of the error function is estimated at each control point B''i0,i1,i2''. The gradient at each control point is denoted by | ||
| − | Equation 5 <br /> <div><br /> </div><div><br /> </div><div><br /> </div><div><br /> </div><div><div align="left"> | + | Equation 5 <br /> <div><br /> </div><div><br /> </div><div><br /> </div><div><br /> </div><div><div align="left"><math> |
| + | \triangledown E(i_0,i_1,i_2) = \left ( \frac {E \left ( i_0+ \Delta x, i_1,i_2 \right ) - E \left (i_0 - \Delta x,i_1,i_2 \right )} {2\Delta x} \right ) , \left ( \frac {E \left ( i_0i_1 + \Delta y, i_2 \right ) - E \left (i_0i_1 - \Delta y,i_2 \right )} {2\Delta y} \right ), | ||
| + | \left ( \frac {E \left ( i_0i_1i_2 + \Delta z \right ) - E \left (i_0i_1i_2 - \Delta z \right )} {2\Delta z} \right ) | ||
| + | </math></div> </div> | ||
The gradient descent step is as follows. The current control point under consideration is B''i0,i1,i2''. The ray originating at this point and having direction of greatest decrease in E is | The gradient descent step is as follows. The current control point under consideration is B''i0,i1,i2''. The ray originating at this point and having direction of greatest decrease in E is | ||
| − | Equation 6 <div align="left"> | + | Equation 6 <div align="left"><math> |
| + | B ^\backprime {i_0,i_1,i_2} (t) = B^\backprime {i_0,i_1,i_2} +tD | ||
| + | </math></div><br /> | ||
where the direction is the unit length vector | where the direction is the unit length vector | ||
| − | <div><div align="left"> | + | <div><div align="left"><math> |
| + | D = \frac {\triangledown E(i_0,i_1,i_2)} {|\triangledown E(i_0,i_1,i_2)|} | ||
| + | </math></div> </div> | ||
| − | and where [[Image:BSplineRegistrationOV_withMath66.jpg]] is computed using | + | and where [[Image:BSplineRegistrationOV_withMath66.jpg]] is computed using equation 5. The idea is to choose t > 0 to minimize |
| − | <div><div align="left"> | + | <div><div align="left"><math> |
| + | e(t) = E (B^\backprime i_0i_1i_2 (t)) | ||
| + | </math></div> </div> | ||
| − | A calculus approach which sets the first derivative to zero and solves for ''t'' yields an expression for ''e(t)'' that is really complicated. Instead, you should choose a set of ''t''-values, ''t''''1'' through ''t''''m'', evaluate ''e(t''''i'''')'' and find the minimum value. Suppose this occurs at ''t''''k''. Replace this in | + | A calculus approach which sets the first derivative to zero and solves for ''t'' yields an expression for ''e(t)'' that is really complicated. Instead, you should choose a set of ''t''-values, ''t''''1'' through ''t''''m'', evaluate ''e(t''''i'''')'' and find the minimum value. Suppose this occurs at ''t''''k''. Replace this in equation 6 to obtain the new location for the control point. |
| − | Only those ''t''-values which do not result in the occurrence of folding in the B-spline transformation are considered. The method described in Section | + | Only those ''t''-values which do not result in the occurrence of folding in the B-spline transformation are considered. The method described in Section "Detect folding" is used to determine if folding occurs for a given set of control point positions. Note that sample ''t0 '' (i.e., ''t=0'') is equivalent to the location of the control point before any movement attempt, and by definition, sample ''t0'' does not cause folding. A test is made to determine whether folding occurs for ''tm'', the extreme sample in the set of chosen ''t-''values. If folding does not occur at ''tm'', then folding does not occur at any of the other ''t-''values between ''t0'' and ''tm''. If folding does occur at ''tm'', then a bisection method is employed to find the ''tf old'' value between ''t0'' and ''tm'' where folding begins to occur. The search for a minimum value of ''e(t)'' by sampling must be limited to the ''t'' < ''t''''f old''. |
=== Error measures === | === Error measures === | ||
| − | All of the error measures between two images defined in this section assume that the two images have the same dimensions. This is the case for the target image | + | All of the error measures between two images defined in this section assume that the two images have the same dimensions. This is the case for the target image T (j0,j1,j2) and registered source image S (j0,j1,j2) = S(k0,k1,k2). |
| − | + | The particular error measures defined here are only concerned with corresponding samples from the two images or histograms of the values of the samples from the two images, and are not concerned with whether the images have two or three dimensions. For simplicity, each image measure will be defined with a single index to access its samples. | |
| + | |||
| + | For more information, refer to [[Cost functions used in MIPAV algorithms]]. | ||
| + | |||
| + | === Least squares measure === | ||
The least squares measure is defined by | The least squares measure is defined by | ||
| − | Equation 7 <br /> <div><div align="left"> | + | Equation 7 <br /> <div><div align="left"><math> |
| + | E_{LS} = \sum_{j}{|S^\prime(j) - T(j)|}^2 | ||
| + | </math></div> </div> | ||
where the summation is over all the indices for the target image voxels. | where the summation is over all the indices for the target image voxels. | ||
| Line 70: | Line 226: | ||
Here, ''S''''`''(''j'') is a registered source image and ''T''(''j'') is a target image. The minimum value of this measure is zero; the maximum value depends on the range of values in the target and registered source images. | Here, ''S''''`''(''j'') is a registered source image and ''T''(''j'') is a target image. The minimum value of this measure is zero; the maximum value depends on the range of values in the target and registered source images. | ||
| − | + | For more information, refer to [[Cost functions used in MIPAV algorithms]]. | |
| + | === Correlation ratio measure === | ||
| + | |||
| + | See also: [[Cost functions used in MIPAV algorithms]]. | ||
The correlation ratio measure is defined by | The correlation ratio measure is defined by | ||
| − | Equation 8 <br /> <div><div align="left"> | + | Equation 8 <br /> <div><div align="left"><math> |
| + | E_{CR}= \frac {\sum_{k} \frac {n_k} {N} Var (S^\prime _k)} {Var (S)} | ||
| + | </math></div> </div> | ||
where | where | ||
| Line 87: | Line 248: | ||
The range of values for this measure is [''0,1'']. | The range of values for this measure is [''0,1'']. | ||
| − | + | === Normalized mutual information measure === | |
The normalized mutual information measure is defined by | The normalized mutual information measure is defined by | ||
| − | Equation 9 <br /> <div><div align="left"> | + | Equation 9 <br /> <div><div align="left"><math> |
| + | E_{NMI} = \frac {H(S^\prime, T)} {H(S^\prime) + H(T)} | ||
| + | </math></div> </div> | ||
where | where | ||
| − | <div><div align="left"> | + | <div><div align="left"><math> |
| + | H(S^\prime, T)= -\sum_{i,j}p_{i,j}log p_{i,j} | ||
| + | </math></div> </div> | ||
is the standard entropy definition for probability pij estimated using the ''(i,j)'' joint histogram bins, and similarly for the marginals ''H(S')'' and ''H(T)''. | is the standard entropy definition for probability pij estimated using the ''(i,j)'' joint histogram bins, and similarly for the marginals ''H(S')'' and ''H(T)''. | ||
| Line 100: | Line 265: | ||
The standard entropy calculation | The standard entropy calculation | ||
| − | <div><div align="left"> | + | <div><div align="left"><math> |
| + | H(S^\prime, T)= -\sum_{k}p_{k}log p_{k} | ||
| + | </math></div> </div> | ||
for an image ''X'' of ''N ''samples and user-selectable ''k'' histogram intensity bins equally distributed over the range of samples in image ''X'' can be rewritten as | for an image ''X'' of ''N ''samples and user-selectable ''k'' histogram intensity bins equally distributed over the range of samples in image ''X'' can be rewritten as | ||
| − | <div><div align="left"> | + | <div><div align="left"> |
| + | <math> | ||
| + | H(X) = -\sum_{k} \frac {n_k} {N} log \left ( \frac {n_k} {N} \right ) | ||
| + | </math></div> </div> | ||
where n''k'' is the histogram value for the k-th intensity bin and ''N'' =<font face="Symbol">S</font> ''k ''n''k''. The computational effort can be reduced by factoring to get | where n''k'' is the histogram value for the k-th intensity bin and ''N'' =<font face="Symbol">S</font> ''k ''n''k''. The computational effort can be reduced by factoring to get | ||
| − | <div><div align="left"> | + | <div><div align="left"><math> |
| + | H(X) = \left ( \frac{-1}{N} \right ) \sum_{k} n_K (logn_k -log N) | ||
| + | </math></div> </div> | ||
where ''log n''''k'' can be a precomputed lookup table of logarithms of integer values. | where ''log n''''k'' can be a precomputed lookup table of logarithms of integer values. | ||
| − | The range of values for this measure is [ | + | The range of values for this measure is [0,1]. |
| + | |||
| + | For more information, refer to [[Cost functions used in MIPAV algorithms]]. | ||
=== Improving performance === | === Improving performance === | ||
| Line 124: | Line 298: | ||
=== Initial placement of control points for identity map === | === Initial placement of control points for identity map === | ||
| − | Referring to | + | Referring to equation 1 for the definition of the B-spline mapping function, the identity map is the one which yields |
| − | <div><br > | + | <div><br ><math> |
| + | M_{j_0j_1j_2} = (\frac {j_0} {p_0-1}), (\frac{j_1} {p_1-1}), (\frac {J_2)} {P_2+1}) | ||
| + | </math>.</div><br /><div align="left"> | ||
This section describes how to initially place the control points to yield this identity map. Since a separate set of B-spline basis functions is defined for each dimension, it happens that the placement of the control points to provide this identity map is computed independently for each dimension. This means that the ''x''-coordinate for each control point initially is determined by the B-spline basis defined for the ''X''-axis, and similarly for other dimensions. | This section describes how to initially place the control points to yield this identity map. Since a separate set of B-spline basis functions is defined for each dimension, it happens that the placement of the control points to provide this identity map is computed independently for each dimension. This means that the ''x''-coordinate for each control point initially is determined by the B-spline basis defined for the ''X''-axis, and similarly for other dimensions. | ||
| Line 134: | Line 310: | ||
For a B-spline basis of degree 1, the initial placement of the control points for the identity map is such that the control point coordinates are uniformly spaced as follows: | For a B-spline basis of degree 1, the initial placement of the control points for the identity map is such that the control point coordinates are uniformly spaced as follows: | ||
| − | Equation 10 <div align="left"> | + | Equation 10 <div align="left"><math> |
| + | B_{i_k} = \frac {i_k} {n_k} | ||
| + | </math></div><br /> | ||
for coordinate ''k''. If the problem is to register images of three dimensions, and the B-spline bases for all three dimensions are selected to have degree 1, then | for coordinate ''k''. If the problem is to register images of three dimensions, and the B-spline bases for all three dimensions are selected to have degree 1, then | ||
| − | Equation 11 <br /> <div><div align="left"> | + | Equation 11 <br /> <div><div align="left"><math> |
| + | B_{i_0, i_1, i_2} = \left ( \frac {i_0}{n_0}, \frac {i_1} {n_1}, \frac {i_2} {n_2} \right ) | ||
| + | </math></div> </div> | ||
| − | For a B-spline basis of degree 2 or larger, the initial placement of the control point coordinates is computed by the method of least squares. Again referring to | + | For a B-spline basis of degree 2 or larger, the initial placement of the control point coordinates is computed by the method of least squares. Again referring to equation 2 for the definition of the B-spline mapping function, the identity map for coordinate ''k'' is |
| − | <div><div align="left"> | + | <div><div align="left"><math> |
| + | \frac {j_k}{p_k-1} = \sum_{i_k=0} ^{n_k}N_{i_k,d_k} \left ( \frac {j_k}{p_k-1} \right ) B_{i_k} | ||
| + | </math></div> </div> | ||
for any target image coordinate j''k'' satisfying 0<= j''k'' <p''k''. | for any target image coordinate j''k'' satisfying 0<= j''k'' <p''k''. | ||
| Line 148: | Line 330: | ||
A system of p''k'' equations above for n''k'' 1 unknowns (i.e., the Bi''k ''coordinate values) is set up in a matrix form A''X'' = ''C'', where | A system of p''k'' equations above for n''k'' 1 unknowns (i.e., the Bi''k ''coordinate values) is set up in a matrix form A''X'' = ''C'', where | ||
| − | <div><div align="left"> | + | <div><div align="left"><math> |
| + | \left ( X_i = B_{i_k} \right ), \left (A_{ji}=N_{i_k,d_k} \left ( \frac {j_k} {p_k-1} \right) \right ),\left (C_j = \frac {j_k} {p_k-1} \right ) | ||
| + | </math></div> </div> | ||
The solution is computed as | The solution is computed as | ||
| − | <div><div align="left"> | + | <div><div align="left"> |
| + | <math> | ||
| + | X = (A^TA)^{-1}A^TC | ||
| + | </math></div> </div> | ||
The repositioning of the control points to yield this identity map is guaranteed not have create folding in the resulting transformation. | The repositioning of the control points to yield this identity map is guaranteed not have create folding in the resulting transformation. | ||
| − | + | === Composition for two-pass registration === | |
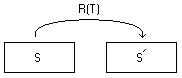
Let ''S'' be a source image and ''T'' be the target image. If the image ''S'' is registered to image ''T'', then image ''S'' becomes the registered source image where ''R(T)'' is the registration mapping. This is graphically shown as: | Let ''S'' be a source image and ''T'' be the target image. If the image ''S'' is registered to image ''T'', then image ''S'' becomes the registered source image where ''R(T)'' is the registration mapping. This is graphically shown as: | ||
| − | [[Image: | + | [[Image:BSplineComposition1.png]] |
For B-spline registration, the ''R(T)'' mapping is based on the selected B-spline basis and control points for each axis. | For B-spline registration, the ''R(T)'' mapping is based on the selected B-spline basis and control points for each axis. | ||
| Line 166: | Line 353: | ||
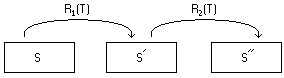
In the case of two-pass registration, the registered source image ''S''' is then registered to the same target image ''T'', but this time using different mapping parameters, i.e., a different set of B-spline basis and control points for the axes. The output of this second registration is a new registered source image ''S"''. Let ''R''''1''''(T)'' be the mapping for the first pass registration and ''R''''2''''(T)'' be the mapping for the second pass registration. This is graphically shown as: | In the case of two-pass registration, the registered source image ''S''' is then registered to the same target image ''T'', but this time using different mapping parameters, i.e., a different set of B-spline basis and control points for the axes. The output of this second registration is a new registered source image ''S"''. Let ''R''''1''''(T)'' be the mapping for the first pass registration and ''R''''2''''(T)'' be the mapping for the second pass registration. This is graphically shown as: | ||
| − | [[Image: | + | [[Image:BSplineComposition2.png]] |
The usefulness of a two-pass registration is that the first pass would apply a coarse-level computation to quickly arrive at an approximate registration, and then the second pass would apply a finer-level computation to continue from the point where the first pass registration finished. The first pass registration may use B-spline bases with fewer control points and a smaller degree. | The usefulness of a two-pass registration is that the first pass would apply a coarse-level computation to quickly arrive at an approximate registration, and then the second pass would apply a finer-level computation to continue from the point where the first pass registration finished. The first pass registration may use B-spline bases with fewer control points and a smaller degree. | ||
| Line 174: | Line 361: | ||
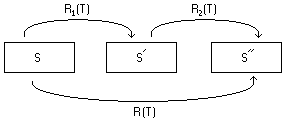
This means defining a mapping ''R(T)'' having the same B-spline bases as the second pass registration mapping ''R''''2''''(T),'' but which maps the original source image ''S'' into the final registered source image ''S''. This is graphically shown as: | This means defining a mapping ''R(T)'' having the same B-spline bases as the second pass registration mapping ''R''''2''''(T),'' but which maps the original source image ''S'' into the final registered source image ''S''. This is graphically shown as: | ||
| − | [[Image: | + | [[Image:BSplineComposition3.png]] |
The ''R(T)'' mapping for the second pass in a two-pass registration is different in that the initial placement of the control points does not yield the identity map to the original source image ''S''. | The ''R(T)'' mapping for the second pass in a two-pass registration is different in that the initial placement of the control points does not yield the identity map to the original source image ''S''. | ||
| Line 182: | Line 369: | ||
=== Deformation === | === Deformation === | ||
| − | The deformation from the nonlinearly registered source image ''S'' to the target image ''T'' can be measured at each sample in the target image by computing the determinant of the Jacobian matrix for the nonlinear transformation. For three dimensions, the nonlinear registration transformation is defined by [[ | + | The deformation from the nonlinearly registered source image ''S'' to the target image ''T'' can be measured at each sample in the target image by computing the determinant of the Jacobian matrix for the nonlinear transformation. For three dimensions, the nonlinear registration transformation is defined by [[#Equation1| Equation 1]]. Since each M''j0j1j2 ''contains normalized 3D coordinates of the position in the source image mapped for each (j0, j1, j2) in the target image, a map image of 3D coordinates can be created that contains these M''j0j1j2 ''source images coordinates (this map image has the same dimensions as the target image). An estimate of the gradient at each sample in this map image is computed using central finite differences at interior samples and forward/backward finite differences at "outer layer" samples. Since each sample in the map image contains 3D coordinates, the estimated gradient at each sample then is a 3x3 matrix of values representing the Jacobian matrix. A single-valued deformation image with the same dimensions as the target image is created which contains the computed determinants of the Jacobian matrices for each sample. |
If no deformation has occurred at a sample, the Jacobian matrix is the identity and its determinant is 1. If the source image is compressed near a sample, the determinant will be less than one. If the source image is expanded near a sample, the determinant will be greater than one. The computation of deformation is unaffected by differences in the dimensions for the source and target images. Because of the constraints on the placement of the control points, a negative determinant should not be possible, which would indicate some type of folding in the mapping. | If no deformation has occurred at a sample, the Jacobian matrix is the identity and its determinant is 1. If the source image is compressed near a sample, the determinant will be less than one. If the source image is expanded near a sample, the determinant will be greater than one. The computation of deformation is unaffected by differences in the dimensions for the source and target images. Because of the constraints on the placement of the control points, a negative determinant should not be possible, which would indicate some type of folding in the mapping. | ||
| − | == | + | == Next == |
| − | + | *[[B-Spline Automatic Registration | B-Spline Automatic Registration - you are here]] | |
| − | + | *[[BSpline registration: Detecting folding]] | |
| − | + | *[[Examples of BSpline registration]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | - | + | *[[User Dialogs in MIPAV | B-Spline Automatic Registration Dialog]] |
| − | + | == See also == | |
| − | + | **[[Optimized automatic registration 3D]] | |
| + | **[[Registration: Landmark-Least Squares]] | ||
| + | **[[Registration: Landmark-TPSpline]] | ||
| + | **[[Registration: Manual 2D Series]] | ||
| + | **[[Registration: Time Series Optimized Automatic Registration]] | ||
| − | + | [[Category:Help]] | |
| − | + | [[Category:Help:Algorithms]] | |
Latest revision as of 18:14, 9 May 2012
This chapter describes the B-spline based registration of images in three dimensions (3D). The description specializes to two dimensions (2D) is in the obvious manner. Chapter is continued on the following pages:
- B-Spline Automatic Registration - you are here
Class implementation for MIPAV
The following classes are part of the mipav/model/structures package:
- B-splineBasis
- B-splineBasisDiscretef
- BSplineLattice2Df
- BSplineLattice3Df
- BSplineRegistrationBasef
- fBSplineRegistration2Df
The following classes are also part of the mipav/model/algorithms/registration package:
- AlgorithmRegBSpline
- AlgorithmRegBSpline2D
- AlgorithmRegBSpline3D
- AlgorithmRegBSpline25D
Background
Let the target image have dimensions <math> (p_o)\,(p_o)\,(p_o) </math> with image indices satisfying <math> 0\le j_0<p_0 </math>, <math> 0\le j_1<p_1 </math>, and <math> 0\le j_2<p_2 </math>. Let the source image have dimensions <math> (q_o)\,(q_o)\,(q_o) </math> with image indices satisfying <math> 0\le k_0<q_0 </math>, <math> 0\le k_1<q_1 </math>, and <math> 0\le k_2<q_2 </math>. The B-spline volume function maps indices <math> j_0,j_1,j_2 </math> via equation 1.
Equation 1M_{j_0, j_1, j_2} = \sum_{i_0=0}^{n_o} \left( N_{i_0},d_0,\frac{j_0}{p_0-1} \sum_{i_1=0}^{n_1} \left( N_{i_1}, \frac{j_1}{p_1-1} \sum_{i_2=0}^{n_2} N_{i_2}, d_2, \frac{j_2}{p_2-1}, B_{i_0, i_1, i_2} \right) \right)
where the <math> N_{i_e, d_e}(u) </math> functions are the B-spline basis functions, and the B values are the control points. The numbers <math>
n_0,n_1,</math> and <math> n_2 </math>, are user selectable, the degrees
<math>
d_0,d_1,</math> and <math> d_2
</math> for the basis functions are user selectable, and the B-spline basis functions are open and uniform.
The control points have the following characteristics:
- Each control point has coordinates from the unit cube. In two dimensions, each control point has coordinates from the unit square.
- The initial placement of the control points depends on the B-spline basis and must yield the identity function; that is,
<math>
M_{j_0j_1j_2} = (\frac {j_0} {p_0-1}), (\frac{j_1} {p_1-1}), (\frac {J_2)} {P_2+1})
</math>. The initial placement of the control points is described in Section "Improving performance".
- A control point is said to be in the outer layer if one of its indexes is either the minimum index (zero) or the maximum index (one less than the number of control points in a given dimension). The position of the control points in the outer layer are fixed as follows:
B_0,i_1,i_2 =(0,y_{i_1},z_{i_2}) </math>
<math> B_{i_0}, 0, i_2 = (\chi_{i_0}, 0, z_{i_2}) </math>
<math> B_{i_0}, i_0, 0 = (\chi_{i_0}, y_{i_1}, 0) </math>
<math> B_{n_0-1}, i_1, i_2 = (1, y_{i_1}, z_{i_2}) </math>
<math> B_{i_0},n_1-1, i_2 = (\chi_{i_0}, 1, z_{i_2}) </math>
<math> B_{i_0},i_1, n_2-1 = (\chi_{i_0}, y_{i_1}, 1) </math>
- This constraint implies that the <math>
0\le k^\prime_w<q_w </math>' 'for all w.
- A control point not in the outer layer is said to be an interior control point. The position of the interior control points is constrained such that its movement must not cause any folding in the B-spline transformation. Folding is defined to occur when there is a negative value anywhere in the computed deformation for the current B-spline transformation. The computation of the deformation is described in Section "Deformation". The method by which folding is detected is described in Section "Detect folding".
Each <math>
M_(j_0)(j_1)(j_2)
</math> contains normalized 3D coordinates (i.e., in the unit cube) that identify a location in the source image corresponding to the sample at <math> (j_0,j_1,j_2) </math> in the target image. The <math>
M_(j_0)(j_1)(j_2)
</math> coordinates are related to sample coordinates in the source image by <math>
M_{j_{0}, j_{1}, j_{2}} =\left( \frac {k^\prime_0}{q_0-1}, \frac{k^\prime_1}{q_1-1}, \frac{k^\prime_2}{q_2-1}\right)
</math> where the output indices <math> k^\prime_0, k^\prime_1, k^\prime_2 </math> are considered to be continuous values; that is, they are not necessarily integer valued. If the source image's samples are <math> s_k\_0,k_1,k_2 </math>, where <math> 0\le k^\prime_w < q_w </math> for all w , we need to evaluate the image at the nonintegral values <math> k^\prime_0, k^\prime_1, k^\prime_2 </math>. We can use trilinear interpolation to do this (use bilinear interpolation in the case of two-dimensional (2D) registration). Let <math> k_w= |k^\prime_w| </math>, the largest integer smaller than <math> k^\prime_w </math>. Define <math> \Delta w = k^\prime_w - k_w </math>. The interpolated image value is:
Equation 3
<math>
U_0 = (1-\Delta_0)(S_{k_0,k_1,k_2}) + (\Delta_0)(S_{k_0 + 1,k_1,k_2})
</math>
<math> U_1 = (1-\Delta_0)(S_{k_0,k_1+1,k_2} + (\Delta_0)(S_{k_0,k_1 + 1,k_2}) </math>
<math> U_2 = (1-\Delta_0)(S_{k_0,k_1,k_2+1} + (\Delta_0)(S_{k_0+1,k_1,k_2+1}) </math>
<math> U_3 = (1-\Delta_0)(S_{k_0,k_1+1,k_2+1} + (\Delta_0)(S_{k_0+1,k_1+1,k_2+1}) </math>
<math> \nu_0 = (1 - \Delta_1)U_0 + (\Delta_1)(U_1) </math>
<math> \nu_1 = (1 - \Delta_1)U_2 + (\Delta_1)(U_3) </math>
<math> S(\kappa_0, \kappa_1, \kappa_2) = (1- \Delta_2)\nu_0 + (\Delta_2)(\nu_1) </math>
If the target image samples are <math> T_{j_0, j_1, j_2} </math>, where <math> 0 \le j_w < p_w </math> for all w, then the source image S is trilinearly interpolated at <math> (k^\prime_0,k^\prime_1, k^\prime_2) </math>, which are the coordinates of <math>
M_(j_0)(j_1)(j_2)
</math>. This means that the currently registered source image, denoted ![]() , has the same dimensions as the target image and can be defined in terms of the target image samples as <math>
S^\prime(j_0,j_1,j_2) = S(k^\prime_0,k^\prime_1, k^\prime_2)
</math>. A measure of error between the two images Sj0,j1,j2 and Tj0,j1 ,j2 can be computed. A number of possible error measure functions are defined in Section 1.2. The goal is to select the control point positions to make the error measure as small as possible. This is done by moving a single control point at a time using gradient descent.
, has the same dimensions as the target image and can be defined in terms of the target image samples as <math>
S^\prime(j_0,j_1,j_2) = S(k^\prime_0,k^\prime_1, k^\prime_2)
</math>. A measure of error between the two images Sj0,j1,j2 and Tj0,j1 ,j2 can be computed. A number of possible error measure functions are defined in Section 1.2. The goal is to select the control point positions to make the error measure as small as possible. This is done by moving a single control point at a time using gradient descent.
The gradient of the error function is estimated for the control point Bi0,i1,i2 by means of finite differences, where changes in the error function are measured for small steps of the control point from its current position in each of the coordinate axis directions. Let ![]() ,
, ![]() and
and ![]() be small step sizes equivalent to one sample increment in the target image,
be small step sizes equivalent to one sample increment in the target image,
\left( \Delta x = \frac{1} {p_0} \right),\left( \Delta y = \frac{1} {p_1} \right),\left( \Delta z = \frac{1} {p_2} \right)
</math>The gradient of the error function is estimated at each control point Bi0,i1,i2. The gradient at each control point is denoted by
Equation 5\triangledown E(i_0,i_1,i_2) = \left ( \frac {E \left ( i_0+ \Delta x, i_1,i_2 \right ) - E \left (i_0 - \Delta x,i_1,i_2 \right )} {2\Delta x} \right ) , \left ( \frac {E \left ( i_0i_1 + \Delta y, i_2 \right ) - E \left (i_0i_1 - \Delta y,i_2 \right )} {2\Delta y} \right ), \left ( \frac {E \left ( i_0i_1i_2 + \Delta z \right ) - E \left (i_0i_1i_2 - \Delta z \right )} {2\Delta z} \right )
</math>The gradient descent step is as follows. The current control point under consideration is Bi0,i1,i2. The ray originating at this point and having direction of greatest decrease in E is
Equation 6B ^\backprime {i_0,i_1,i_2} (t) = B^\backprime {i_0,i_1,i_2} +tD
</math>where the direction is the unit length vector
D = \frac {\triangledown E(i_0,i_1,i_2)} {|\triangledown E(i_0,i_1,i_2)|}
</math>and where ![]() is computed using equation 5. The idea is to choose t > 0 to minimize
is computed using equation 5. The idea is to choose t > 0 to minimize
e(t) = E (B^\backprime i_0i_1i_2 (t))
</math>A calculus approach which sets the first derivative to zero and solves for t yields an expression for e(t) that is really complicated. Instead, you should choose a set of t-values, t'1 through t'm, evaluate e(t'i') and find the minimum value. Suppose this occurs at t'k. Replace this in equation 6 to obtain the new location for the control point.
Only those t-values which do not result in the occurrence of folding in the B-spline transformation are considered. The method described in Section "Detect folding" is used to determine if folding occurs for a given set of control point positions. Note that sample t0 (i.e., t=0) is equivalent to the location of the control point before any movement attempt, and by definition, sample t0 does not cause folding. A test is made to determine whether folding occurs for tm, the extreme sample in the set of chosen t-values. If folding does not occur at tm, then folding does not occur at any of the other t-values between t0 and tm. If folding does occur at tm, then a bisection method is employed to find the tf old value between t0 and tm where folding begins to occur. The search for a minimum value of e(t) by sampling must be limited to the t < t'f old.
Error measures
All of the error measures between two images defined in this section assume that the two images have the same dimensions. This is the case for the target image T (j0,j1,j2) and registered source image S (j0,j1,j2) = S(k0,k1,k2).
The particular error measures defined here are only concerned with corresponding samples from the two images or histograms of the values of the samples from the two images, and are not concerned with whether the images have two or three dimensions. For simplicity, each image measure will be defined with a single index to access its samples.
For more information, refer to Cost functions used in MIPAV algorithms.
Least squares measure
The least squares measure is defined by
Equation 7E_{LS} = \sum_{j}{|S^\prime(j) - T(j)|}^2
</math>where the summation is over all the indices for the target image voxels.
Here, S'`(j) is a registered source image and T(j) is a target image. The minimum value of this measure is zero; the maximum value depends on the range of values in the target and registered source images.
For more information, refer to Cost functions used in MIPAV algorithms.
Correlation ratio measure
See also: Cost functions used in MIPAV algorithms. The correlation ratio measure is defined by
Equation 8E_{CR}= \frac {\sum_{k} \frac {n_k} {N} Var (S^\prime _k)} {Var (S)}
</math>where
- Var(S) is the variance of the registered source image S.
- k is the number of intensity histogram bins equally distributed over the range of intensity values of the target image T.
- S'k'' is the k-th isoset defined as the set of intensities in registered source image S' at positions where the intensity in target image T is in the k-th intensity bin.
- nk is the number of elements in the set Sk, such that N =Sk ''n'k.
- N is the number of samples in the target image T which is the same number of samples in the registered source image S'.
- Var(Sk) is the variance of the values in the set Sk.
The range of values for this measure is [0,1].
Normalized mutual information measure
The normalized mutual information measure is defined by
Equation 9E_{NMI} = \frac {H(S^\prime, T)} {H(S^\prime) + H(T)}
</math>where
H(S^\prime, T)= -\sum_{i,j}p_{i,j}log p_{i,j}
</math>is the standard entropy definition for probability pij estimated using the (i,j) joint histogram bins, and similarly for the marginals H(S') and H(T).
The standard entropy calculation
H(S^\prime, T)= -\sum_{k}p_{k}log p_{k}
</math>for an image X of N samples and user-selectable k histogram intensity bins equally distributed over the range of samples in image X can be rewritten as
<math> H(X) = -\sum_{k} \frac {n_k} {N} log \left ( \frac {n_k} {N} \right )
</math>where nk is the histogram value for the k-th intensity bin and N =S k nk. The computational effort can be reduced by factoring to get
H(X) = \left ( \frac{-1}{N} \right ) \sum_{k} n_K (logn_k -log N)
</math>where log n'k can be a precomputed lookup table of logarithms of integer values.
The range of values for this measure is [0,1].
For more information, refer to Cost functions used in MIPAV algorithms.
Improving performance
The gradient descent applied to a control point at a time can be quite slow. Performance can be improved by taking advantage of the local control aspect of using B-splines. Since only one control point is being moved at a time, the local control aspect of using B-splines means that only some of the registered source image values will be different. Note that for an image of a given size, the number of image values, under local control, affected by moving a control point decreases as the number of control points increases.
One performance improvement can be achieved by precomputing the B-spline basis function values once for each possible sample for each dimension. Since the registration occurs by transforming the source image into the space of the target image, all samples for B-spline basis function evaluation always occur at the discrete sample coordinates for the target image. Since the number of target images samples for a dimension is xed, the B-spline basis function will be evaluated on the [0, 1] interval at equally spaced intervals (we are using open, uniform B-splines). For each dimension, a 2D array is created which stores B-splines basis function evaluations for each sample with the weight associated with each control point. Because of local control, many of these weights will be zero indicating that a sample is not affected by a particular control point. In the process of creating this 2D array of precomputed basis function evaluations, the index range of samples affected by each control point can be determined. The algorithm to determine this range does not examine the weights as they are computed; instead, the range of control points affecting a single sample are determined from the computed knot index and the known B-spline degree.
Another performance improvement involves maintaining intermediate error measure calculations. For example, in the case of the least squares error measure, an image is maintained of the current error calculations, that is, the target image subtracted from the current registered source image. A cumulative total error value is also maintained, which is the sum of the squared error values for all current values in the error image. When a control point is moved, the old values that are being replaced are first subtracted from the total error, and then the new values to be stored are added to the total error. Similar approaches are performed for the correlation ratio and normalized mutual information error measures such as storing cumulative histogram values and images which contain predetermined histogram bin indexes.
Initial placement of control points for identity map
Referring to equation 1 for the definition of the B-spline mapping function, the identity map is the one which yields
<math>
M_{j_0j_1j_2} = (\frac {j_0} {p_0-1}), (\frac{j_1} {p_1-1}), (\frac {J_2)} {P_2+1})
</math>.This section describes how to initially place the control points to yield this identity map. Since a separate set of B-spline basis functions is defined for each dimension, it happens that the placement of the control points to provide this identity map is computed independently for each dimension. This means that the x-coordinate for each control point initially is determined by the B-spline basis defined for the X-axis, and similarly for other dimensions.
Let k be the coordinate for which the control point identity map is being computed for the associated B-spline basis. Let nk be the number of control points defined for that B-spline basis. Let ik be the index of the control point coordinate such that 0<= ik <= nk. The goal is to compute the coordinate values Bik for all ik where each coordinate value is in the [0,1] range.
For a B-spline basis of degree 1, the initial placement of the control points for the identity map is such that the control point coordinates are uniformly spaced as follows:
Equation 10B_{i_k} = \frac {i_k} {n_k}
</math>for coordinate k. If the problem is to register images of three dimensions, and the B-spline bases for all three dimensions are selected to have degree 1, then
Equation 11B_{i_0, i_1, i_2} = \left ( \frac {i_0}{n_0}, \frac {i_1} {n_1}, \frac {i_2} {n_2} \right )
</math>For a B-spline basis of degree 2 or larger, the initial placement of the control point coordinates is computed by the method of least squares. Again referring to equation 2 for the definition of the B-spline mapping function, the identity map for coordinate k is
\frac {j_k}{p_k-1} = \sum_{i_k=0} ^{n_k}N_{i_k,d_k} \left ( \frac {j_k}{p_k-1} \right ) B_{i_k}
</math>for any target image coordinate jk satisfying 0<= jk <pk.
A system of pk equations above for nk 1 unknowns (i.e., the Bik coordinate values) is set up in a matrix form AX = C, where
\left ( X_i = B_{i_k} \right ), \left (A_{ji}=N_{i_k,d_k} \left ( \frac {j_k} {p_k-1} \right) \right ),\left (C_j = \frac {j_k} {p_k-1} \right )
</math>The solution is computed as
<math> X = (A^TA)^{-1}A^TC
</math>The repositioning of the control points to yield this identity map is guaranteed not have create folding in the resulting transformation.
Composition for two-pass registration
Let S be a source image and T be the target image. If the image S is registered to image T, then image S becomes the registered source image where R(T) is the registration mapping. This is graphically shown as:
For B-spline registration, the R(T) mapping is based on the selected B-spline basis and control points for each axis.
In the case of two-pass registration, the registered source image S' is then registered to the same target image T, but this time using different mapping parameters, i.e., a different set of B-spline basis and control points for the axes. The output of this second registration is a new registered source image S". Let R'1'(T) be the mapping for the first pass registration and R'2'(T) be the mapping for the second pass registration. This is graphically shown as:
The usefulness of a two-pass registration is that the first pass would apply a coarse-level computation to quickly arrive at an approximate registration, and then the second pass would apply a finer-level computation to continue from the point where the first pass registration finished. The first pass registration may use B-spline bases with fewer control points and a smaller degree.
Although the two-pass registration can be performed in the manner just described, it is desirable to have a final registration between the original source image S and the target image T.
This means defining a mapping R(T) having the same B-spline bases as the second pass registration mapping R'2'(T), but which maps the original source image S into the final registered source image S. This is graphically shown as:
The R(T) mapping for the second pass in a two-pass registration is different in that the initial placement of the control points does not yield the identity map to the original source image S.
Instead, the initial placement of the control points for R(T) yields the output of the R'1'(T) mapping. This is achieved by initializing the R'2'(T) registration mapping in the normal manner which provides an initial placement of its control points to yield the identity map from the registered source image S. The initial placement of the control points for the R(T) mapping then are the initial placement of the control points for R'2'(T) mapped through R'1'(T).
Deformation
The deformation from the nonlinearly registered source image S to the target image T can be measured at each sample in the target image by computing the determinant of the Jacobian matrix for the nonlinear transformation. For three dimensions, the nonlinear registration transformation is defined by Equation 1. Since each Mj0j1j2 contains normalized 3D coordinates of the position in the source image mapped for each (j0, j1, j2) in the target image, a map image of 3D coordinates can be created that contains these Mj0j1j2 source images coordinates (this map image has the same dimensions as the target image). An estimate of the gradient at each sample in this map image is computed using central finite differences at interior samples and forward/backward finite differences at "outer layer" samples. Since each sample in the map image contains 3D coordinates, the estimated gradient at each sample then is a 3x3 matrix of values representing the Jacobian matrix. A single-valued deformation image with the same dimensions as the target image is created which contains the computed determinants of the Jacobian matrices for each sample.
If no deformation has occurred at a sample, the Jacobian matrix is the identity and its determinant is 1. If the source image is compressed near a sample, the determinant will be less than one. If the source image is expanded near a sample, the determinant will be greater than one. The computation of deformation is unaffected by differences in the dimensions for the source and target images. Because of the constraints on the placement of the control points, a negative determinant should not be possible, which would indicate some type of folding in the mapping.
Next
- B-Spline Automatic Registration - you are here