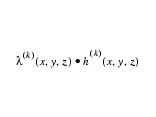Microscopy: Blind Deconvolution

Blind Deconvolution is a technique, which permits recovery of the target object from a set of blurred images in the presence or a poorly determined or unknown Point Spread Function (PSF). In optical microscopy, blind deconvolution is used to remove the blurring induced by the limited aperture of the microscope objective. Instead of subtracting blur from the image, a part of the light contribution to the blurred pixels is reassigned to the correct in-focus location in the image.

To properly reassign the intensity values in the chosen image, the imaging system must be modeled. The model includes known attributes such as the objective numerical aperture, the refractive index of the sample immersion medium, and the wavelength of the light used to image the sample (either reflected light or fluorescence).

An optical imaging system is then modeled as a convolution of the target image with a PSF. Here, the PSF is assumed to have a Gaussian shape. This convolution is considered to produce the blurred image. To de-blur the image, the convolution is reversed, and the blurred image is deconvolved with the same PSF. Images can be deconvolved using a PSF that is measured directly by imaging certain types of samples, such as fluorescent beads; or the PSF can be estimated based on the optical parameters of the microscope (imaging system). In blind deconvolution, an estimated PSF is used, and both the estimated (de-blurred) image and the PSF image are recovered by the deconvolution process.

Blind deconvolution works through an iterative process. After the deconvolution step, the estimated image produced by the deconvolution is corrected by comparing it to the original blurred image. The same correction is also applied to the PSF image. The corrected estimated image and PSF are later used in the next deconvolution step, and are further refined through the successive iterations. .

An initial estimate for the target image is set to be the converted input image, while the initial estimate for the PSF is determined as a Gaussian kernel of size 3x3 for 2D images or 3x3x3 for 3D images. Once the estimate and PSF images have been initialized the algorithm computes new estimates with the iterative process as shown below. Refer to equations 1 - 3:

Equation 1

Equation 2

Equation 3

Here:


	is the original input image
	is the estimated input image
	is the estimated PSF
	is an unconstrained PSF
	represents convolution

This algorithm uses a numerical method to calculate a maximum-likelihood estimation of the input image using the steps described in equations 1-3.

An initial estimate of the input image is made;
This estimate is, then, convolved with a theoretical PSF calculated based on the optical parameters of the imaging system. See "Computing convolution"
The resulting blurred estimate is compared with the input image;
After that, a correction is computed and employed to generate a new estimate. The same correction is also applied to the PSF, generating a new PSF estimate.
The PSF estimate is constrained to form the new PSF estimate for the next iteration. Refer to "PSF constraints" below;
In the further iterations, the PSF estimate and the image estimate are updated together.

Computing convolution

Convolution is computed by taking the Fast Fourier Transformation (FFT) of the images, multiplying in Fourier space, and then taking the inverse FFT. Refer to Section "Fast Fourier Transformation for more information about FFT.

If the extents of the input image are not a power of 2, the nearest power of 2 for each dimension is estimated and the input image is resampled to the power of 2 for efficient computation of FFT.

PSF constraints

It is possible to incorporate some prior knowledge about the PSF into the algorithm. It has been shown that the solution to the PSF has to be constrained in some way so that reconstructions had resemblance to the true object and true PSF. Hence, the following constraints are applied to the PSF image before the next iteration:

Unit summation - all intensity values in the PSF image must sum to 1.
Hourglass - limits the energy of the PSF so that portions of the background intensity, which lie outside an hourglass (or disk for 2D), are not assigned to the PSF.
Band-limit and missing cone - constraint the Fourier transform of the PSF (the optical transfer function) to be band-limited.
Non negativity - ensures that the PSF has no negative values.

Image types

You can apply this algorithm to color and grayscale, 2D and 3D images.

Note: For color images, the input color image is, first, converted into grayscale. After that, the deconvolution process is performed on the grayscale representation of the image. And in the final processing step, the color values are restored by iterating once through the deconvolution process for each source channel using the estimated image and estimated PSF of the grayscale representation. All images are converted to floating point representation for processing. Refer to Figure 1.

**Figure 1. The original color image (A), the intermediate grayscale image (B), and the final estimate color image after 10 iterations (C).**

Notes

Blind deconvolution eliminates the need to acquire an empirical PSF, and can be used for both microscopy and non-microscopy images. Refer to Figure 2 that shows the Jupiter image.

**Figure 2. The original image of Jupiter in grayscale (A), the estimate image after five iterations (B), and the final estimate after 10 iterations (C).**

References

Refer to the following sources for more information about blind deconvolution.

Holmes, T.J., Maximum Likelihood Image Restoration Adapted for Noncoherent Optical Imaging, JOSA-A, 5(5): 666-673, 1988.

---, Bhattacharyya, S., Cooper, J., Hanzel, D., Krishnamurthi, V., Lin, W., Roysam, B., Szarowski, D., Turner, J., Light Microscopic Images Reconstructed by Maximum Likelihood Deconvolution, Ch. 24, Handbook of Biological Confocal Microscopy, J. Pawley, Plenum, 1995.

---, Liu, Y., Image Restoration for 2D and 3D Fluorescence Microscopy, Visualization in Biomedical Microscopy, A. Kriete, VCH, 1992.

---, Blind Deconvolution of Quantum-Limited Noncoherent Imagery, JOSA-A, 9: 1052 - 1061, 1992

Useful links

http://www.mediacy.com/aqi/index.asp

http://micro.magnet.fsu.edu/primer/digitalimaging/deconvolution/deconvolutionhome.html

http://micro.magnet.fsu.edu/primer/digitalimaging/deconvolution/deconintro.html

http://micro.magnet.fsu.edu/primer/digitalimaging/deconvolution/deconalgorithms.html

[1]http://www.hamangia.freeserve.co.uk/how/index.html

Applying the Maximum Likelihood Iterative Blind Deconvolution algorithm

To apply the algorithm, complete the following steps:

Open an image of interest.
From the main MIPAV menu select Algorithms > Microscopy > Restoration > Maximum Likelihood Iterated Blind Deconvolution.
The Maximum Likelihood Iterated Blind Deconvolution dialog box appears.

Complete the information in the dialog box.

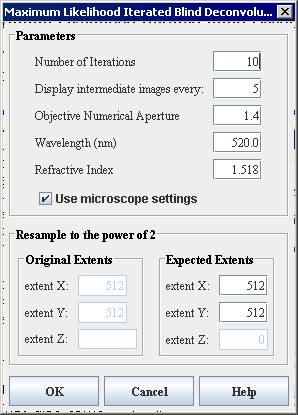
**Figure 3. The Maximum Likelihood Iterated Blind Deconvolution dialog box**
Number of Iterations	Enter the number of times to iterate through the blind-deconvolution process. The default value is 10 iterations.
Display intermediate image every	Enter the frequency of display for intermediate images here. The default value is 5, which means that the intermediate images will be displayed every five iterations. Displaying intermediate results allows the user to save a series of images and adjust the PSF parameters to produce the better result. Note that the best result may also come from an earlier iteration.
Objective Numerical Aperture	Enter the numerical aperture of the microscope objective used in the imaging system. The default value is 1.4.
Wavelength (nm)	Enter the wavelength of the light used to image the sample, or the wavelength of the light fluorescence, in nanometers. The default wavelength is 520 nanometers.
Refractive Index	This is the refractive index of the sample immersion medium. The default value is 1.518 (the refractive index of common microscope immersion oils).
Use microscope settings	Uncheck this box to turn off the microscope-specific optical parameters. However, if the box is checked and the theoretical PSF derived from the microscope parameters contains all zero values, the algorithm will automatically disable the checkbox. Refer to Section "PSF constraints" for more information. By default, the box is checked on.
Resample to the power of 2
Original Extents (extent X, extent Y, and extent Z)	Displays the original extents of the input image. If the image is not a 3D image, then the extent Z field is empty. A user cannot edit these values.
Expected Extents (extent X, extent Y, and extent Z)	Displays the expected extents of the image to the nearest power of 2. If the image is not a 3D image, then the extent Z field is empty and non-editable. It is recommended to not change the expected extents values as these are the most efficient values to the nearest power of 2.
OK	Applies the algorithm according to the specifications in this dialog box.
Cancel	Disregards any changes that you made in the dialog box and closes this dialog box.
Help	Displays online help for this dialog box.

Press OK to run the algorithm.
The algorithm begins to run, and a pop-up window appears with the status: Computing iterative blind deconvolution. See Figure 4.

4. A status pop-up window.
While running, the algorithm produces several intermediate images or estimates which appear on the screen. The number of estimates depends on two parameters: 1) the number of iterations and 2) the frequency of appearing of intermediate images. These parameters are set in the Number of Iterations: and Display intermediate images every: fields of the dialog box.
If the Use Microscope Settings: box was checked, but the PSF derived from the microscope parameters contains all zero values, the algorithm automatically displays the warning as shown in Figure 5, and then, disables the checkbox. Refer to "PSF constraints" to learn more about PSF constraints.

Figure 5. The PSF warning.
When the algorithm finishes running, the status window closes, and the intermediate and final results appear in new windows.

Selecting the algorithm parameters

Careful parameter selection must be done for the Blind Deconvolution algorithm to produce good results. To find an optimal set of parameters values, apply this algorithm repeatedly on the same image (or a set of images) that you want to process with different parameter values and with a reasonable number of intermediate imaged selected.

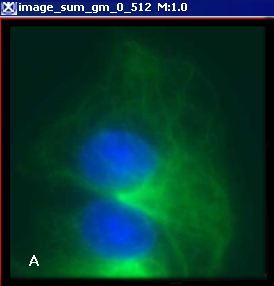
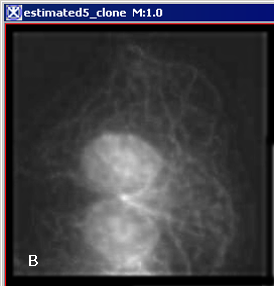
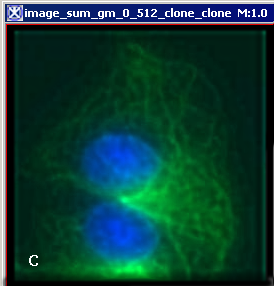
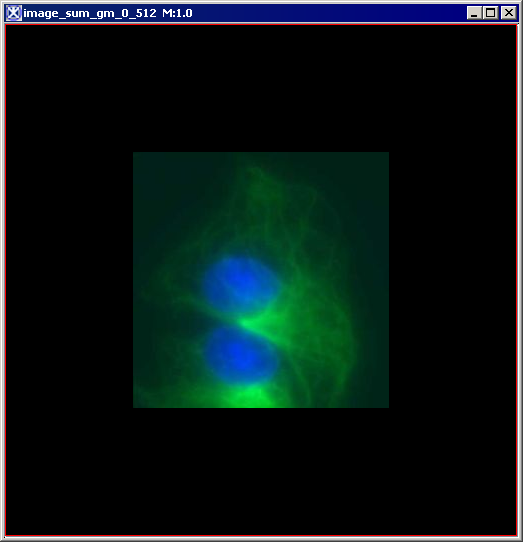
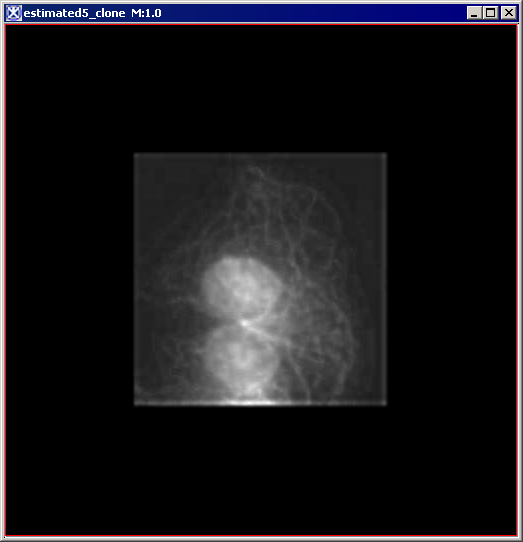
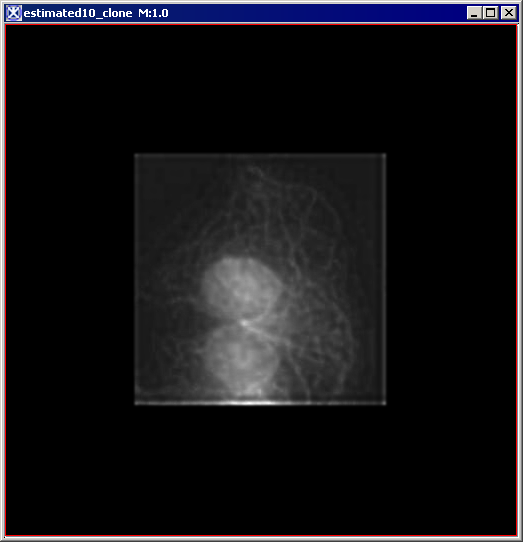
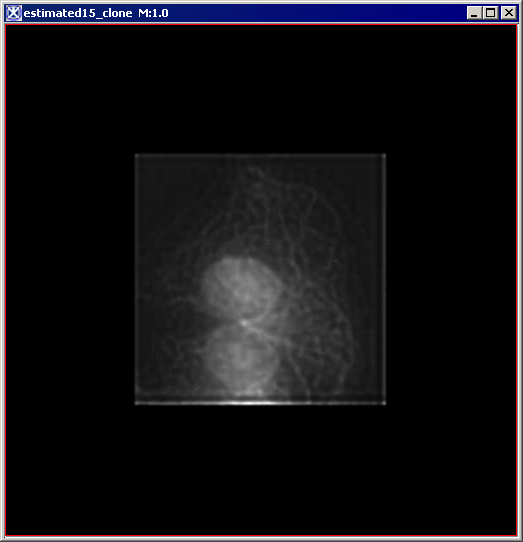
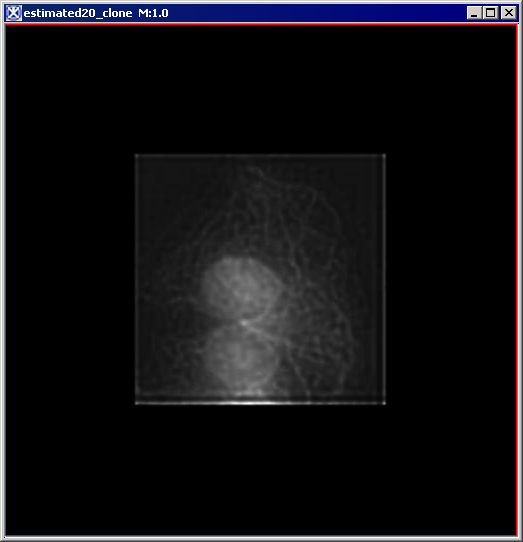
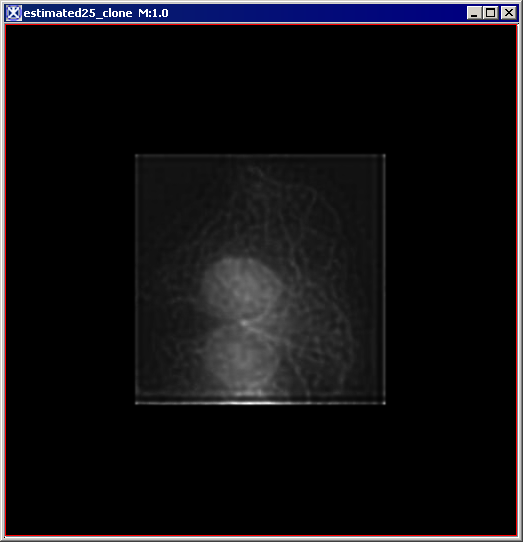
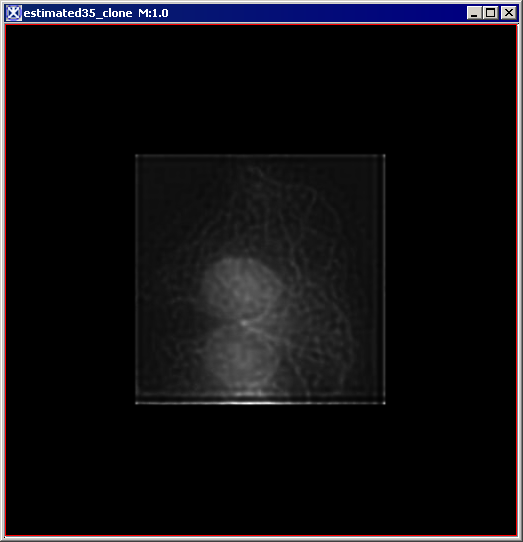
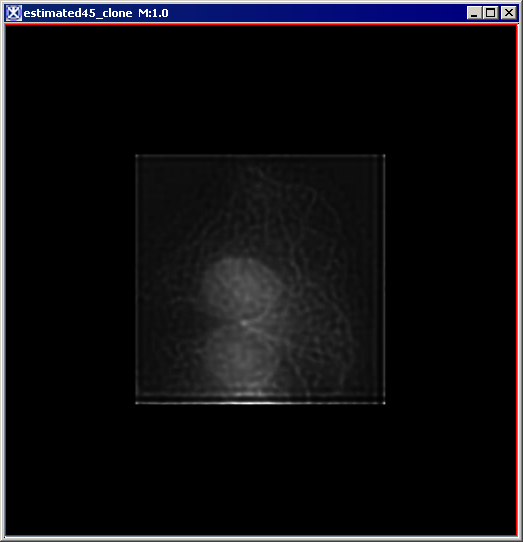
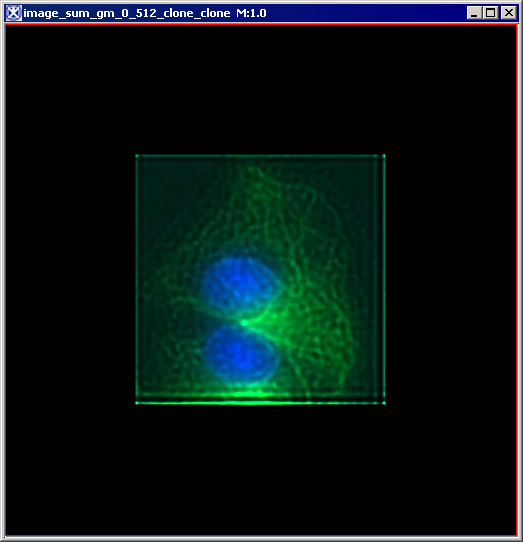
Figure 6 below shows images that were produced from running the Blind Deconvolution algorithm with the default parameters against a color microscopy image. The final image was produced after 50 iterations. The intermediate images appear every five iterations.

However, the initial image was in color the intermediate images (estimates) appear in grayscale. Also note that the name of the intermediate image includes the word "estimate" and the number of the iteration.

Note: Hourglass constraint: and Band-limit and missing cone constraint: uses the Objective Numerical Aperture, Wavelength, and Refractive Index parameters provided by the user to determine the size and shape of the PSF.