Filters (Wavelet): Thresholding
The wavelet transform or wavelet analysis is a solution to overcome the shortcomings of the Fourier transform. In wavelet analysis, the modulated window is shifted along the signal, and for every position, the spectrum is calculated. Then, this process is repeated many times with a slightly shorter (or longer) window for every new cycle. In the end, the result appears as a collection of time-frequency representations of the signal, all with different resolutions. Since the modulated window is fully scalable, this solves the signal-cutting problem which arises in the Fourier transform.
Because the result appears as a collection of time-frequency representations of the signal, we can speak of a multi resolution analysis. However, in the case of wavelets, we normally do not speak about time-frequency representations, but about time-scale representations, scale being in a way the opposite of frequency, because the term frequency is reserved for the Fourier transform.
Contents
Background
Outline of the algorithm
The image is expanded so that all dimensions are powers of 2 and there is zero padding going past each original boundary by the coefficient number equals 2.
- The image is transformed into wavelet coefficients using the threshold type selected by the user.
- The signal reconstructed from wavelet coefficients.
- Then, an inverse wavelet transform is performed.
- The image is stripped down to its original size. The data is clamped so as not to exceed the bounds of the data type of the image into which it is imported.
| Note: the forward and inverse Daubechies wavelet transform routines are taken from Numerical Recipes in C, The Art of Scientific Computing 2nd edition by William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery, Cambridge University Press, 1997, Chapter 13.10, pp. 591 606. |
Image types
2D and 3D black and white images.
Applying the Wavelet Thresholding algorithm
To use this algorithm, do the following:
- To apply the algorithm, do the following:
- Open an image of interest.
- Navigate to Algorithms > Filters Wavelet > Thresholding.
- In the Wavelet Thresholding dialog box that appears, complete the following fields:
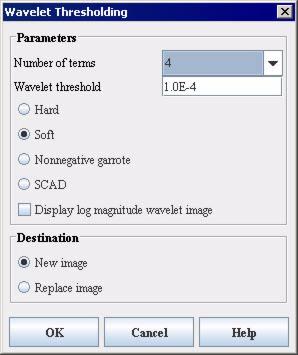
- In the Number of Terms list box, select 4, 12 or 20. Numbers of Terms here means the number of wavelet vanishing moments or an approximation order;
- In the Wavelet Threshold box, specify the threshold value;
- To specify the threshold type, use the radio buttons: Hard, Soft, Nonnegative garrote, and SCAD;
- To display the log magnitude wavelet image, check the corresponding box. Displaying this image will help you to adjust the algorithm settings;
- Select the destination, use the New Image option to view the result image in a new frame, or use the Replace Image option o view the result image in the same frame.
- Press OK. The algorithm begins to run and the new image appears in the specified frame.
Wavelet Thresholding dialog box
|
Number of terms
|
- this is the number of wavelet vanishing moments or an approximation order. Select 4, 12 or 20.
|
|
|
Wavelet threshold
|
- use to specify the threshold value
| |
|
Hard Soft Nonnegative garrote SCAD
|
- use these radio buttons specify the threshold type.
| |
|
Display log magnitude wavelet image
|
- check this box to display the log magnitude wavelet image. Displaying this image will help you to adjust the algorithm settings.
| |
|
New image
|
use this to view the result image in a new frame.
| |
|
Replace image
|
use this to view the result image in the same frame.
| |
|
OK
|
Applies the algorithm according to the specifications in this dialog box.
| |
|
Cancel
|
Disregards any changes that you made in the dialog box and closes this dialog box.
| |
|
Help
|
Displays online help for this dialog box.
| |