DTI Color Display
A common problem in biomedical sciences is the in vivo identification and analysis of anatomical structures. The DTI Color Display plug-in introduces a novel technique to visualize nerve fiber tracts in diffusion-weighted magnetic resonance imaging data. The method uses the improved diffusion tensor-based Directionally Encoded Color (DEC) schemes which can be used, for example, to identify and display white matter fiber tracts in the human brain.
Contents
Background
The method takes as an input indices of diffusion anisotropy and the principal directions of diffusion (eigenvectors of diffusion tensor D), which characterize specific features of the diffusion process. And then, it uses a color (RGB and/or HSV) representation of the components of the eigenvector associated with the largest eigenvalue of the diffusion tensor (Vmax) weighted by some measure of diffusion anisotropy. This technique provides an effective way to display the directions of anisotropic structures in a single brain image, because:
- The principal directions of diffusion provide information on the spatial orientation of anisotropic structures that may be useful to further characterize tissue structural anatomy.
- Anisotropy measures yield information about the structure of normal and pathological white matter.
There are three issues or three sources of misinterpretation in the DEC schemes that DTI Color Display method improves:
- Antipodal symmetry of the eigenvectors of D, refer to Section Antipodal Symmetry of the Eigenvectors of D
- Nonlinear effects of the display device, refer to Section Color processing
- Properties of human color vision, also refer to Section Color processing
Antipodal Symmetry of the Eigenvectors of D
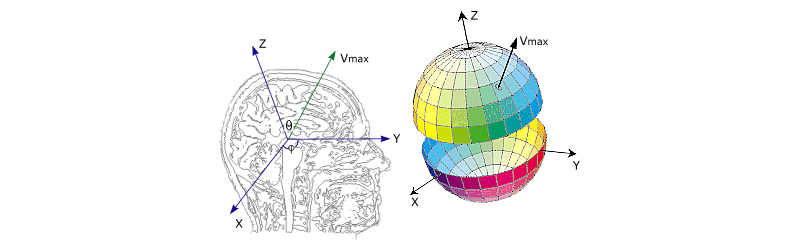
The method is based on assumptions that the orientation of fibers is described by the diffusion tensor eigenvector associated with the largest eigenvalue, Vmax and the parallel and anti-parallel vectors convey the same information. Thus, to have a unique vector representation, the vectors have to be mapped to only one hemisphere in a spherical coordinate system. The plane that divides this spherical coordinate system into two hemispheres, e.g., the plane of discontinuity can be positioned in an arbitrary direction; however, within this plane, fiber orientation will still be represented by two antipodally symmetric vectors Vmax and -Vmax.[[1]]
To reduce these discontinuity artifacts, the method uses a spherical coordinate system fixed to defined anatomical landmarks and independent from the laboratory reference frame in which the tensor dataset is acquired. Within that anatomical coordinate system the eigenvector Vmax is a unit vector completely determined by its polar theta and azimuthal phi angles that are defined as shown in Figure 1. A particular color representation is shown on a unit sphere, which is called the color representation sphere.
Only the vectors expressed in the upper hemisphere, e.g. z' more or equal to 0 or theta' in a range of [0, Pi/2] and the xy plane is the plane of discontinuity, are used for unique color representation. The lower hemisphere is just an antipodally symmetric copy of the upper hemisphere. Refer to Figure 1 in which the color representation sphere is split along the plane of discontinuity. The brightness of a DEC map is weighted by a measure of diffusion anisotropy.[2]
The following considerations were also used to design the color representation sphere:
- Color differences are proportional to actual differences in direction, characterized either by the Euclidian distance between vectors or by the angle between them.
- Only the directional information contained in the D is displayed, and the representation is not affected by parameters related to the magnitude of diffusivity, such as Trace D or diffusion coefficients.
- Commonly identifiable color groups (e.g., red, green, blue, yellow, cyan, magenta, etc.) are associated with a characteristic direction (e.g., direction along x, y, z, and directions bisecting the xy, yz, xz planes).
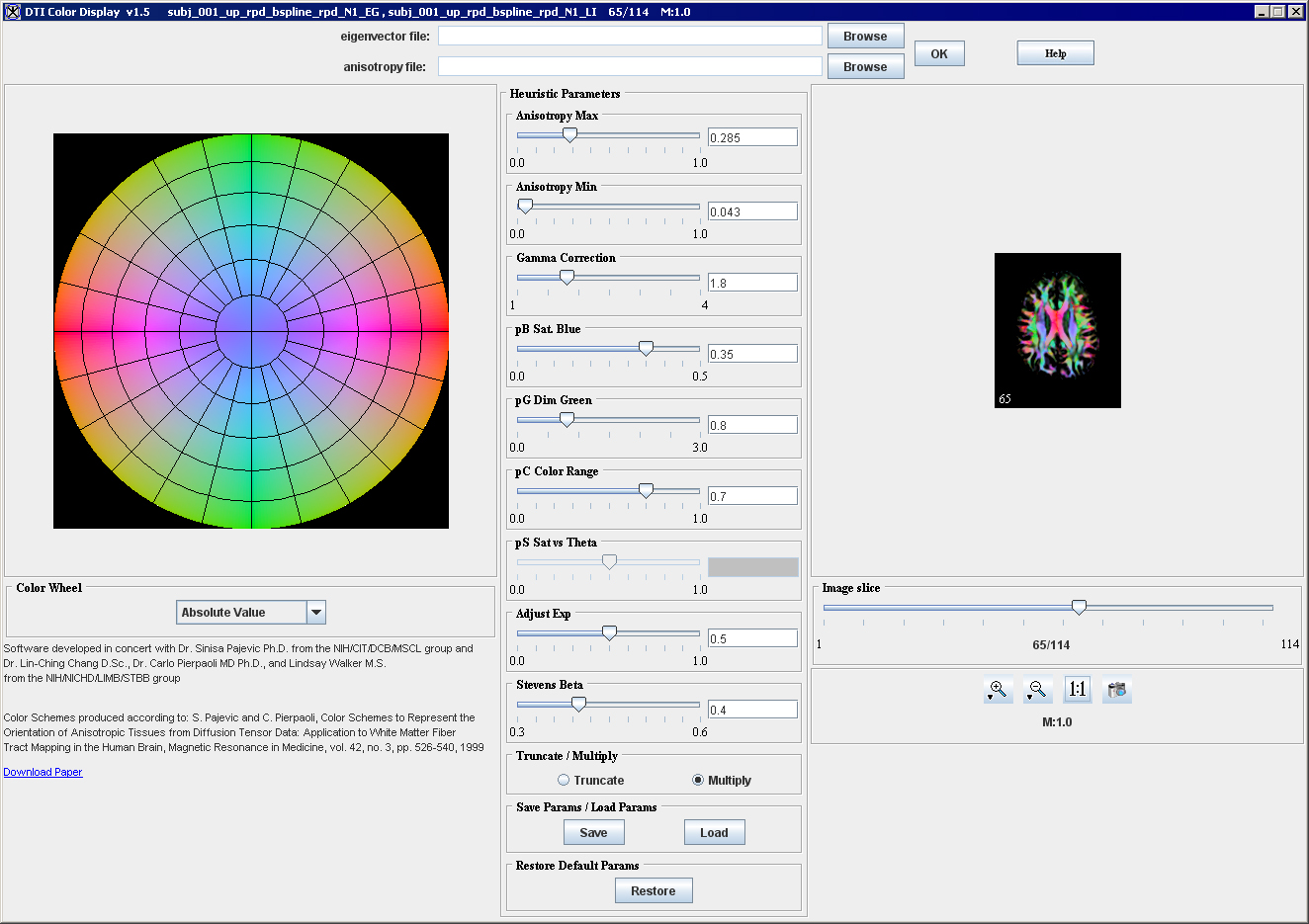
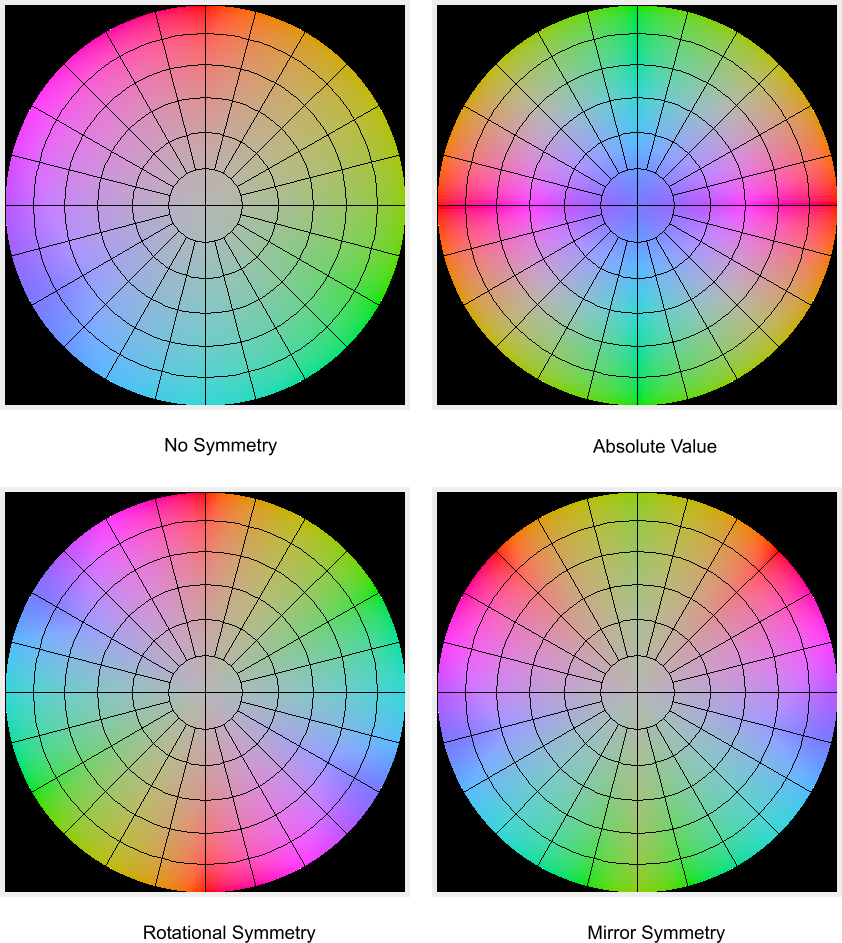
The method allows different directions in the color maps to be represented with the same color if some form of symmetry exists between these directions. However, it causes an orientational ambiguity, because the color representation of orientation is not unique, in some situations using such symmetries is justified by existing symmetries in the human anatomy. With regard to which type of symmetry is used, the method offers the following options: No Symmetry, Rotational Symmetry, Mirror Symmetry, and Absolute Value. See Figure 6.
|
Proper rotations should be done to convert image data from the laboratory frame of reference to the specified anatomical frame of reference before applying the method. See also Section Importance of midsagittal alignment. |
No Symmetry
This representation is implemented by relating the azimuthal angle of the vector phi to color hue and the polar angle theta less or equal Pi/2 to color saturation. For HSV scheme (H=Hue, S=Saturation, V=Value) the following equations are used:
Equation 1|
<math> H = (\phi - \phi_R + 2\pi)mod(2\pi) </math> <math> S = \frac {sin(p_s\theta)} {sin(\frac {p_s\pi}{2})} </math> <math> V=1 </math> |
Where, phi'R is the phi angle of the vector Vmax lying in the xy plane that will be represented in a pure red color, and pS is an heuristic parameter that takes values in the interval [0,1]. When pS < 0, S is approximately a linear function of theta. No Symmetry representation is unique because a particular color describes a single direction, but it suffers from discontinuity artifacts.
Rotational Symmetry
In this scheme, any vector and its pair rotated by 180� around the z axis have the same color representation, e.g. Vmax(theta, phi) = Vmax(\theta, phi Pi) or Vmax(vx,vy,vz) = Vmax(-vx,-vy,-vz). This representation is implemented in a fashion similar to the No Symmetry approach, but with the constraint H(phi) = H(phi Pi).
Equation 2|
<math>H=2(\phi -\phi_R + 2\pi)mod2\pi</math> |
Where, phi'R is the phi angle of the vector lying in the xy plane that will be represented in a pure red color. pS in the interval [0,1] is the same heuristic parameter as used for No Symmetry and equations for S and V are also the same that were used for No Symmetry. See also equation 1.
Rotational Symmetry scheme removes the discontinuity artifacts but does not provide a unique representation of directions and is, also, perceptually highly nonuniform.
Mirror Symmetry
The mirror symmetry representation scheme implies that any two vectors that are mirror images of each other relative to the yz plane of the anatomical frame of reference will have the same color representation, e.g. Vmax(-vx,vy,vz) = Vmax(vx,vy,vz).
Equation 3|
<math>H = 2((\phi - \phi_R + \pi)mod \pi)</math> |
Where, phi is an azimuthal angle of Vmax(|vx|,vy,vz). Mirror symmetry exists between many structures in the left and the right brain hemispheres. Equations for S and V are also the same that were used for No Symmetry, refer to equation 1.
Absolute Value
The Absolute Value scheme implies that the sign of any vector is unimportant; only the absolute value is important. This yields a simple representation in RGB color space in which RGB components are associated with the absolute value of the components of the vector, e.g.
Equation 4|
<math>R_I =|V_x|, G_I = |v_y|, B_I = |v_z|</math> |
Where RI, GI, and BI are the RGB components of the color representation of Vmax,which are defined in the interval (0,1). See also Figure 2.
Color circles
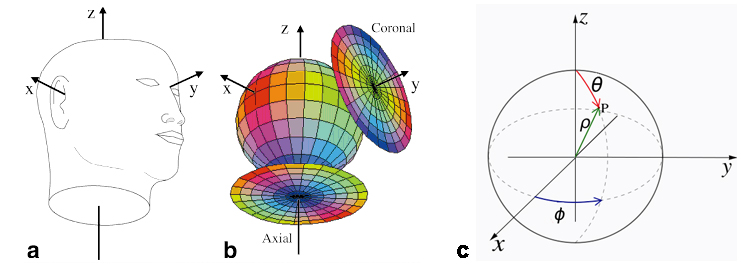
The method uses color circles to relate a chosen color representation sphere with its corresponding fiber orientation. The color circles are constructed by projecting a chosen color representation sphere onto viewing plane using the equal area Lambert's projection. According to the standard convention for viewing MR images, for axial images the representation color sphere is viewed from below (negative z axis of our anatomical coordinate system pointing at the viewer, see Figure 2-a) and for coronal images from the front (positive y axis pointing at the viewer, see Figure 2-b. See also Figure 6.3]
In Figure 2, the orientation of a structure represented with a given color, can be approximately obtained from the color circle by placing one end of a pencil, whose length is approximately equal to the radius of the circle, at the center of the circle and the other end right above the corresponding color.
Building color circles
Figure 2 shows a grid of parallels and meridians added to the circle at 15 degree intervals to indicate the angles theta'v (angle at which the structure is positioned relative to the viewing direction) and phi'v (angle within the viewing plane). Here, phi'v and theta'v are related to the 2D cylindrical coordinates rho and of the equal area color circle as rho=2sin(theta'v'/2) and phi=phi'v as shown in Figure 2.
Color processing
The color processing sequence provided by the method aims at faithfully representing 3D antipodally symmetric vector data, taking into account artifacts associated with particular color display and human color perception. The final goal is that the differences in orientation of such data be proportional to the perceived color differences, as much as that is possible. Since color perception properties, as well as those of antipodally symmetric data, do not allow this to be achieved precisely, the method resorts to approximate schemes using symmetries in data, then it provides tools for correcting the direct color representation using red, green and blue shifts, which aim to equalize different perceptual qualities of those primary colors. Then intensity scaling corrects for our non-uniform perception of luminosity, and finally the gamma correction should be applied to correct for the common non-linearity effect introduced by different color display.
Color processing heuristic parameters
Anisotropy Max and Min are used to set the Anisotropy filter. After the filter is set, only structures where the Anisotropy index was larger than anisotropy min and smaller than anisotropy max are represented, the others are truncated and set to black.
Gamma Correction is used to encode RGB values into luminosity produced by the device, e.g. your computer monitor.
pB Sat.Blue is used to decrease the saturation of blue hue to achieve better uniformity of perceived brightness for different hue values (e.g. red, green, and blue), and more faithful representation of diffusion anisotropy. It is also used as a basis for calculation brightness of red color.
pG Dim Green is used to adjust brightness for green color.
pC Color Range. pC Color Range = 0 yields the maximal range of colors without regard to uniform brightness. pC Color Range = 1 reduces the range of colors, but allows a more faithful representation of anisotropy and a more uniform color representation.
pS Sat vs. Theta is used to modify the dependence between the saturation and the angle theta.
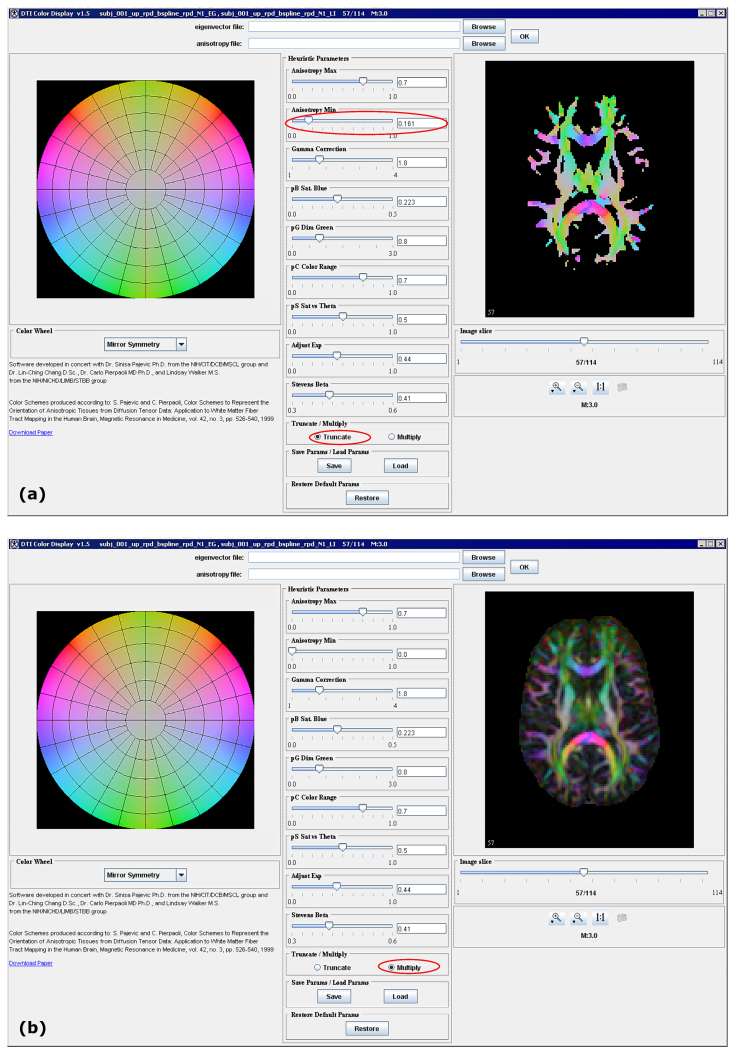
Adjust Exp is used to modify the nonlinear relationship between the perceived brightness and the anisotropy measure. The algorithm uses two types of anisotropy filters in color representations. See also Figure 3.
- In the first one, each of the color components is, first, normalized based on the anisotropy min and max values, e.g. newIntensityValue =(value - anisotropyMin)/(anisotropyMax - anisotropyMin), and then the normalized value is multiplied to a weighting factor equals AdjustExp/StevensBeta. This corresponds to the Multiply option activated in the DTI Color Display dialog box, refer to Figure 3- (b).
- In the second one, only structures where the lattice index was larger than anysotropy min are represented, the others are truncated and set to black. This corresponds to the Truncate option activated in the DTI Color Display dialog box, refer to Figure 3- (a).
Stevens law exponent or StephensBeta which employs the simple nonlinear relationship between the true luminosity of monochromatic light and its perceived brightness, is also treated as heuristic parameter, i.e. it can be adjusted.
Blue, red and green shifts
Uniform brightness is important to view the directional information and the degree of anisotropy simultaneously. In other situations, when the degree of anisotropy is less important one may use a larger range of colors. This is governed by the parameter pC Color Range.
To preserve uniform brightness, the method, first, shifts blue toward the white point according to the following equations:
Equation 5|
<math> R_S=C_B + (1-C_B)R_I </math> <math> G_S=C(B_I) + (1-C_B) G_I </math> <math> B_S=B_I </math> <math> C_B=max \left [ \frac {3} {2} p_B (b-\frac {1}{3})p_C,0 \right] </math> <math> b=\frac {B_I} {R_I+G_I+B_I} </math> |
Where RS, GS, and BS are shifted intensities for red, green and blue components, pB represents the pB Sat.Blue parameter and pC represents pC Color Range. See also Color processing heuristic parameters.
Then, the algorithm performs the red shift in the same manner, but using the smaller pB Sat.Blue, e.g. pB for red shift = pB/4.
And finally, it performs the green shift:
It calculates new shifted intensities for red, green and blue components taking into account the following heuristic parameters: pG Dim Green, pC Color Range, and StephensBeta. See also Color processing heuristic parameters.
Gamma correction
The default values for the gamma correction exponent and StephensBeta are as follows: gamma = 2.2 and StephensBeta = 0.4. However, the method treats them as heuristic parameters, i.e., they can be empirically adjusted. See also Figure 3.
Importance of midsagittal alignment
In real life, the anatomic coordinate system and the reference system for image display do not necessarily coincide, i.e., axial, coronal, and sagittal images are not lying in the xy, xz, and yz planes of the anatomical coordinate system, respectively. In such case, the color coordinate system appears shifted relative to the color circle grid and the above proposed symmetries in color representation (e.g. rotational symmetry and mirror symmetry) would not be easily seen on the color circle. If the misalignment between the anatomical coordinate system and the reference system for image display is severe, images should be rotated and interpolated before applying the method.
Image Types
The algorithm works with any image types supported by MIPAV. However, in order to run the algorithm you should provide two files: an eigenvector file and an anisotropy file. The eigenvector file should be 4D image file with nine time slices, where the first three slices contain the principal eigenvector information. The anisotropy file should be 3D file with anisotropy value range (0,1). The files must have the same 3D dimensionality.
References
Sinisa Pajevic and Carlo Pierpaoli [1999]. "Color Schemes to Represent the Orientation of Anisotropic Tissues From Diffusion Tensor Data: Application to White Matter Fiber Tract Mapping in the Human Brain", Magnetic Resonance in Medicine, vol. 42, pp 526---540.
Applying DTI Color Display
- Install the plug-in.
- Then select Plugins > General > DTI Color Display. The DTI Color Display dialog box opens displaying the Absolute Value color wheel.
- In the dialog box, select the eigenvector and anisotropy files.
- Click OK. The image appears in the Image window.
- Use the Image slice slider to select the slice of interest.
- Select the color wheel which you would like to apply to the image. Note that:
- Absolute Value yields a simple representation in RGB color space in which RGB components are associated with the absolute value of the components of the diffusion vector.
- In No Symmetry scheme, a particular color describes a single direction, but this representation suffers from discontinuity artifacts.
- Rotational Symmetry scheme removes the discontinuity artifacts but does not provide a unique color representation of directions and is, also, perceptually highly nonuniform.
- Mirror Symmetry implies that any two vectors that are mirror images of each other relative to the yz plane of the anatomical coordinate system will have the same color representation. See also Figure 6.
Then, use the Heuristic Parameters sliders to adjust the parameters to achieve the most satisfactory image representation. See also Section Color processing heuristic parameters.
[1]In statistics, directional data with such antipodal symmetry are referred to as axial data.
[2]Pi = 3.14159265