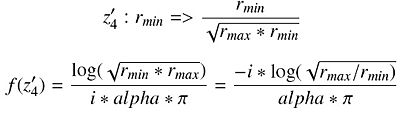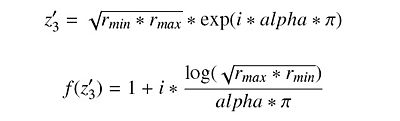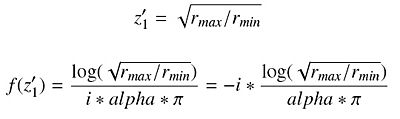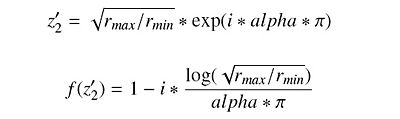Difference between revisions of "Transform: Conformal Mapping Algorithms"

Revision as of 14:14, 20 August 2012

The methods described in this document use conformal mapping to transform points in a circular sector, circle, ellipse, or nearly circular region to points in a circle or rectangle.

Background

A conformal mapping, is a transformation w=f(z) that preserves local angles. An analytic function is conformal at any point where it has a nonzero first derivative. A complex function is analytic on a region R if it is complex differentiable at every point in R. In a conformal mapping, in any small neighborhood the relative angle and shape are preserved.

Circular Sector to Rectangle

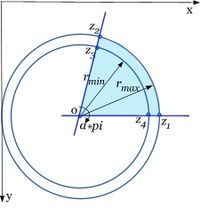
The algorithm uses a 2D conformal mapping to convert a circular sector, defined by four user points at the sector corners, to a rectangle of the user specified size. The circular sector has an inner radius <math>r_{min}</math>, an outer radius <math>r_{max}</math>, and extends over an angle <math>theta = \alpha* \pi</math> radians, with <math>0 \le \alpha \le 1</math>.

Let, <math>z_1</math> and <math>z_2</math> belong to <math>r_{max}</math>, and <math>z_3</math> and <math>z_4</math> belong to <math>r_{min}</math>. The mapping to the user specified rectangle is performed in the following steps (1-6):

Step 1

The maximum radius can be facing to the top, bottom, right, or left. So the algorithm, first, determines which of 4 orientations is present.

Calculating the center of the circle to which the circular segment belongs

Step 2

Calculating the center of the circular segment. The center is calculated as a point <math>(x_c, y_c)</math> where two lines <math>(z_3, z_2)</math> and <math>(z_4, z_1)</math> cross. Therefore,

Equation 1

<math> x_c=\frac {x_3 * y_2) - (x_2 * y_3)} {(x-3 -x_2)} - \frac {(x_4 * y_1) - (x_1 * y_4)} {x_4 - x_1)} </math> <math> y_c = x_c \frac {y_4 -y_1} {x_4 -x_1} + \frac {(x_4 * y_1) - (x_1 * y_4)}{(x-4 - x_1)} </math>

Step 3

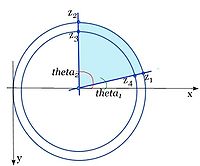
Calculating the angle of the sector in radians.

Transform Conformal Mapping : Calculating the angle of the circular segment

The angle is calculated as follows theta = theta2 - theta1.

For the maximum radius facing to the left, we must take into account the discontinuity of the angle at the negative x axis. The angle changes from <math>-\pi to \pi</math>, so the equation for <math>\theta</math> is now:

<math> \theta = abs(\theta1) + abs(\theta2) - 2.0 * \pi </math>

The angle <math>\theta1</math> is along the line from center to <math>z_4 to z_1</math> in <math> -\pi to \pi </math> radians:

<math> \tan(\theta_1) = \frac{((y_1 - y_4)}{(x_1 - x4_)} => \theta_1 = \arctan{(y_1 - y_4)}{(x_1 - x_4)}</math>

the angle <math>theta_2</math> is along the line from center to <math>z_3 to z_2</math> in <math> -\pi to \pi </math> radians:

<math>\tan(\theta_2)= \frac{(y_2 - y_3)}{(x_2 - x_3)} => \theta_2 = \arctan\frac{(y_2 - y3_)}{(x_2 - x_3)}</math>

Step 4

For the conformal mapping, it requires that <math>r_{max} > 1 and 0 < r_{min} < 1</math>. Refer to "A Domain Decomposition Method for Conformal Mapping onto a Rectangle" Remark 4.7 (see "References" ). The transformation theory is based on a mathematical crosscut along the unit circle.

Therefore, the algorithm divides all the distances from the circular center by <math>\sqrt{r_{max}* r_{min}}</math>. It produces a value of r so that <math>1 < r <\sqrt{r_{max}* r_{min}}</math>

Step 5

To convert a circular sector to a rectangle, the algorithm uses the following transformation function

Equation 2

<math>w = f(z) = u + iv = \frac{\log(z)}{(i*\alpha* \pi)}</math>

Let <math>z =r*\exp(i*\theta)</math>

Then,

Equation 3

<math>w = \log \frac{(r*\exp(i*\theta))}{(i*\alpha* \pi)}</math> =>

<math> w= \frac{\theta}{(\alpha* \pi)} - i*\frac{\log(r)}{(\alpha* \pi)}</math>

<math> u = \frac{\theta}{(\alpha* \pi)}</math>,

<math> v = -\frac{\log(r)}{(\alpha* \pi)}</math>

Since conformal mapping requires that <math>f(z)</math> must be analytic on all points, the Cauchy-Riemann equations must be satisfied and <math>f'(z)</math> must not equal zero.

Satisfying the Cauchy-Riemann equations

Suppose that <math>f(z)=f(x+iy)=u(x,y)+iv(x,y)</math> is differentiable at the point z0=x0+iy0. Then, the partial derivatives of u and v exist at the point (x0, y0), and

Equation 4

<math> f'_x (z_0)=\lim _{\vartriangle x \to 0}\frac{\vartriangle z}{\vartriangle x} </math>

<math> f'_x(z_0) = \lim _{\vartriangle x \to 0} (\frac{\vartriangle u_x (x_0, y_0)+ i \vartriangle v_x (x_0, y_0)}{\vartriangle x}) = \lim _{\vartriangle x \to 0} (\frac{\vartriangle u_x (x_0, y_0)}{\vartriangle x} + \frac {i \vartriangle v_x (x_0, y_0)}{\vartriangle x}) = \frac {du}{dx} + i\frac{dv}{dx} </math>

<math> f'_x (z_0)=\lim _{\vartriangle x \to 0}\frac{\vartriangle z}{\vartriangle y} </math>

<math> f'_x(z_0) = \lim _{\vartriangle y \to 0} (\frac{\vartriangle u_y (x_0, y_0)+ i \vartriangle v_y (x_0, y_0)}{i \vartriangle y}) = \lim _{\vartriangle y \to 0} (\frac{\vartriangle v_y (x_0, y_0)}{\vartriangle y} - i \frac {\vartriangle u_y (x_0, y_0)}{\vartriangle y}) = \frac {dv}{dy} - i\frac{du}{dx} </math> Equating the real and imaginary parts gives

Equation 5

<math> u_x (x_0, y_0) = v_y (x_0, y_0)</math>

and

<math> u_y (x_0, y_0)= - v_x (x_0, y_0)</math>

The Cauchy-Riemann equations in polar form are:

Equation 6

<math> du/dr = (1/r)(dv/d\theta)</math>

<math> -dv/dr = (1/r) (du/d\theta)</math>

The first equation gives zero on both sides and the second equation gives <math>(\alpha* \pi)/r</math> on both sides, so the Cauchy-Riemann equations hold.

Satisfying the non zero first derivative

Equation 7

<math>f'(z) = 1/(i*\alpha* \pi *z)</math>,

<math> f'(z)=!0 </math> except at infinity.

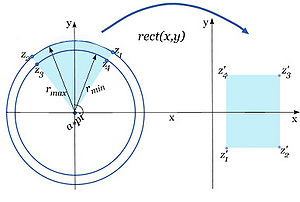
Step 6

Now, the algorithm performs a conformal mapping from the circular segment to a rectangle of width 1 and height <math>log(r_{max}/r_{min})/\theta</math>. Values for f(z1), f(z2), f(z3), and f(z4) are as follows:

Note: In the equations below "alpha" stays for <math>\alpha</math>.

The region inside a circular sector is mapped to a rectangle: z1 is the upper right point on r_max, z2 is the upper left point on r_max, z3 is the lower left point on r_min, and z4 is the lower right point on r_min

Equation 8

Equation 9

Equation 10

Equation 11

Step 7

Then, the rectangle from step 6 is linearly scaled to a rectangle of user specified xDim and yDim. In cases when the maximum radius faces to the top, this gives us the following values for z1', z2', z3'and z4':

z1'= (xDim-1, 0),

z2'= (0, 0),

z3'= (0, yDim-1),

z4'= (xDim-1, yDim-1)

Note that the linear scaling of one rectangle to another is not a conformal mapping unless the width and height are scaled by the same factor.

Transformation: Circle to Rectangle

The user inputs 2 point VOIs. The first point is located at the center of the circle. The second point can be any point located on the actual circle

The algorithm uses a 2D conformal mapping to convert a circle to a rectangle of the user specified size. The circle has the radius r.

The user inputs 2 point VOIs. The first point is located at the center of the circle. The second point can be any point located on the actual circle. The user also inputs the X and Y dimensions (xDimDest and yDimDest) of the output image. See Figure 10. The algorithm performs three mappings to go from the circular area specified by the user to an output rectangle.

Mapping 1

It maps from the destination rectangle to a rectangle centered on the origin. This is the mapping from a rectangle with the edge points (0,0), (xDimDest-1, 0), (xDimDest-1, yDimDest-1), (0, yDimDest-1) to a rectangle with the edge points (-K,Kp), (K,Kp), (K,-Kp), (-K,-Kp).

Where K is the complete elliptic integral of the first kind using the modulus and Kp is the complete elliptic integral of the first kind using the complementary modulus:

<math> complementary_modulus = \sqrt {1 - m^2} </math>

where, the modulus m belongs to the interval [0,1] and is arbitrarily chosen as 0.5.

Transformation: Ellipse to Circle

Transformation: Nearly Circular Region to Circle

Applying the algorithms

Circular Sector to Rectangle

Circle to Rectangle

Ellipse to Circle

Nearly Circle to Circle

References

See also:

For the time being, please refer to the MIPAV HTML help Algorithms/TransformConformalMapping.html