Difference between revisions of "Transform: Conformal Mapping Algorithms"
m |
m (→Equation 5) |
||
| Line 88: | Line 88: | ||
====== Equation 5 ====== | ====== Equation 5 ====== | ||
| − | <math> u_x (x_0, y_0) = v_y (x_0, y_0)<math> | + | <math> u_x (x_0, y_0) = v_y (x_0, y_0)</math> |
and | and | ||
| Line 94: | Line 94: | ||
<math> u_y (x_0, y_0)= - v_x (x_0, y_0)</math> | <math> u_y (x_0, y_0)= - v_x (x_0, y_0)</math> | ||
| − | The Cauchy-Riemann equations in polar form are: | + | The Cauchy-Riemann equations in polar form are: |
====== Equation 6 ====== | ====== Equation 6 ====== | ||
Revision as of 16:41, 17 August 2012
The methods described in this document use conformal mapping to transform points in a circular sector, circle, ellipse, or nearly circular region to points in a circle or rectangle.
Contents
Background
A conformal mapping, is a transformation w=f(z) that preserves local angles. An analytic function is conformal at any point where it has a nonzero first derivative. A complex function is analytic on a region R if it is complex differentiable at every point in R. In a conformal mapping, in any small neighborhood the relative angle and shape are preserved.
Circular Sector to Rectangle
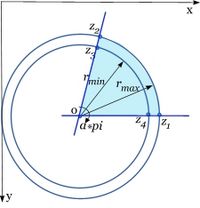
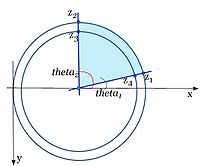
The algorithm uses a 2D conformal mapping to convert a circular sector, defined by four user points at the sector corners, to a rectangle of the user specified size. The circular sector has an inner radius <math>r_{min}</math>, an outer radius <math>r_{max}</math>, and extends over an angle <math>theta = \alpha* \pi</math> radians, with <math>0 \le \alpha \le 1</math>.
Let, <math>z_1</math> and <math>z_2</math> belong to <math>r_{max}</math>, and <math>z_3</math> and <math>z_4</math> belong to <math>r_{min}</math>. The mapping to the user specified rectangle is performed in the following steps (1-6):
1. The maximum radius can be facing to the top, bottom, right, or left. So the algorithm, first, determines which of 4 orientations is present.
2. Calculating the center of the circular segment. The center is calculated as a point <math>(x_c, y_c)</math> where two lines <math>(z_3, z_2)</math> and <math>(z_4, z_1)</math> cross. Therefore,
Equation 1
<math> x_c=\frac {x_3 * y_2) - (x_2 * y_3)} {(x-3 -x_2)} - \frac {(x_4 * y_1) - (x_1 * y_4)} {x_4 - x_1)} </math> <math> y_c = x_c \frac {y_4 -y_1} {x_4 -x_1} + \frac {(x_4 * y_1) - (x_1 * y_4)}{(x-4 - x_1)} </math>
3. Calculating the angle of the sector in radians.
The angle is calculated as follows theta = theta2 - theta1.
For the maximum radius facing to the left, we must take into account the discontinuity of the angle at the negative x axis. The angle changes from <math>-\pi to \pi</math>, so the equation for <math>\theta</math> is now:
<math> \theta = abs(\theta1) + abs(\theta2) - 2.0 * \pi </math>
The angle <math>\theta1</math> is along the line from center to <math>z_4 to z_1</math> in <math> -\pi to \pi </math> radians:
<math> \tan(\theta_1) = \frac{((y_1 - y_4)}{(x_1 - x4_)} => \theta_1 = \arctan{(y_1 - y_4)}{(x_1 - x_4)}</math>
the angle <math>theta_2</math> is along the line from center to <math>z_3 to z_2</math> in <math> -\pi to \pi </math> radians:
<math>\tan(\theta_2)= \frac{(y_2 - y_3)}{(x_2 - x_3)} => \theta_2 = \arctan\frac{(y_2 - y3_)}{(x_2 - x_3)}</math>
4. For the conformal mapping, it requires that <math>r_{max} > 1 and 0 < r_{min} < 1</math>. Refer to "A Domain Decomposition Method for Conformal Mapping onto a Rectangle" Remark 4.7 (see "References" ). The transformation theory is based on a mathematical crosscut along the unit circle.
Therefore, the algorithm divides all the distances from the circular center by <math>\sqrt{r_{max}* r_{min}}</math>. It produces a value of r so that <math>1 < r <\sqrt{r_{max}* r_{min}}</math>
5. To convert a circular sector to a rectangle, the algorithm uses the following transformation function
Equation 2
<math>w = f(z) = u + iv = \frac{\log(z)}{(i*\alpha* \pi)}</math>
Let <math>z =r*\exp(i*\theta)</math>
Then,
Equation 3
<math>w = \log \frac{(r*\exp(i*\theta))}{(i*\alpha* \pi)}</math> =>
<math> w= \frac{\theta}{(\alpha* \pi)} - i*\frac{\log(r)}{(\alpha* \pi)}</math>
<math> u = \frac{\theta}{(\alpha* \pi)}</math>,
<math> v = -\frac{\log(r)}{(\alpha* \pi)}</math>
Since conformal mapping requires that <math>f(z)</math> must be analytic on all points, the Cauchy-Riemann equations must be satisfied and <math>f'(z)</math> must not equal zero.
Satisfying the Cauchy-Riemann equations
Suppose that <math>f(z)=f(x+iy)=u(x,y)+iv(x,y)</math> is differentiable at the point z0=x0+iy0. Then, the partial derivatives of u and v exist at the point (x0, y0), and
Equation 4
<math> f'_x (z_0)=\lim _{\vartriangle x \to 0}\frac{\vartriangle z}{\vartriangle x} </math>
<math> f'_x(z_0) = \lim _{\vartriangle x \to 0} (\frac{\vartriangle u_x (x_0, y_0)+ i \vartriangle v_x (x_0, y_0)}{\vartriangle x}) = \lim _{\vartriangle x \to 0} (\frac{\vartriangle u_x (x_0, y_0)}{\vartriangle x} + \frac {i \vartriangle v_x (x_0, y_0)}{\vartriangle x}) = \frac {du}{dx} + i\frac{dv}{dx} </math>
<math> f'_x (z_0)=\lim _{\vartriangle x \to 0}\frac{\vartriangle z}{\vartriangle y} </math>
<math> f'_x(z_0) = \lim _{\vartriangle y \to 0} (\frac{\vartriangle u_y (x_0, y_0)+ i \vartriangle v_y (x_0, y_0)}{i \vartriangle y}) = \lim _{\vartriangle y \to 0} (\frac{\vartriangle v_y (x_0, y_0)}{\vartriangle y} - i \frac {\vartriangle u_y (x_0, y_0)}{\vartriangle y}) = \frac {dv}{dy} - i\frac{du}{dx} </math> Equating the real and imaginary parts gives
Equation 5
<math> u_x (x_0, y_0) = v_y (x_0, y_0)</math>
and
<math> u_y (x_0, y_0)= - v_x (x_0, y_0)</math>
The Cauchy-Riemann equations in polar form are:
Equation 6
<math> du/dr = (1/r)(dv/d\theta)</math>
<math> -dv/dr = (1/r) (du/d\theta)</math>
The first equation gives zero on both sides and the second equation gives (alpha* Pi)/r on both sides, so the Cauchy-Riemann equations hold.
Satisfying the non zero first derivative
Equation 7
<math>f'(z) = 1/(i*\alpha* \pi *z)</math>,
<math> f'(z)=!0 </math> except at infinity.
Now, the algorithm performs a conformal mapping from the circular segment to a rectangle of width 1 and height <math>log(r_{max}/r_{min})/\theta</math>. Values for f(z1), f(z2), f(z3), and f(z4) are as follows:
Transformation: Circle to Rectangle
Transformation: Ellipse to Circle
Transformation: Nearly Circular Region to Circle
Applying the algorithms
Circular Sector to Rectangle
Circle to Rectangle
Ellipse to Circle
Nearly Circle to Circle
References
See also:
For the time being, please refer to the MIPAV HTML help Algorithms/TransformConformalMapping.html