Difference between revisions of "Interpolation methods used in MIPAV"
m (→B-spline basis interpolations) |
m (→B-spline basis interpolations) |
||
| Line 79: | Line 79: | ||
<math> | <math> | ||
| − | N_{i,1} (t) | + | N_{i,1} (t) = \left\{ |
| + | \begin{array}{l l} | ||
| + | 1 & \quad t_{i} \leq t < t_{i+1}\\ | ||
| + | 0 & \quad otherwize\\ | ||
| + | \end{array} \right. | ||
</math> | </math> | ||
'''See also:''' [[Optimized automatic registration 3D]] | '''See also:''' [[Optimized automatic registration 3D]] | ||
[[Category:Help:Stub]] | [[Category:Help:Stub]] | ||
Revision as of 19:17, 8 May 2012
This article is a stub. It needs improvement.
The registration and transformation algorithms implemented in MIPAV resampes images (if needed) using an interpolation scheme, where anisotropic voxels (or pixels for 2D images) are resampled into isotropic 1 mm cubic voxels. New voxel values are computed using a weighted combination of existing voxel values within a defined neighborhood of the new voxel location. The following interpolation methods are available in this implementation of the registration technique, including Bilinear, Trilinear, B-spline 3-rd order, B-spline 4-th order, Cubic Lagrangian, Quintic Lagrangian, Heptic Lagrangian, and Windowed sinc.
Contents
Bilinear Interpolation
Bilinear interpolation considers the closest 2 x 2 neighborhood of known pixel values surrounding the unknown pixel. It then takes a weighted average of these 4 pixels to arrive at its final interpolated value. This results in smoother looking images. It performs linear interpolation in one direction, and then again in the other direction. Although each step is linear in terms of position and the sampled values the interpolation as a whole is not linear but rather quadratic in the sample location.
Where to use
Bilinear interpolation can be used in transformations, where the perfect pixel matching is impossible, so one can calculate and assign appropriate intensity values to pixels. Unlike other interpolation techniques (e.g. nearest neighbor and bicubic interpolation), bilinear interpolation uses only the 4 nearest pixel values which are located in diagonal directions from a given pixel in order to find the appropriate color intensity values of that pixel.
Example
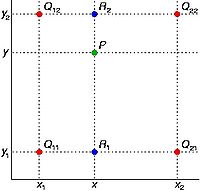
In the figure shown on your right, red dots Q12, Q22, Q11 and Q21 represent the known pixels and the green dot P is the pixel we wish to interpolate. Note that the known pixel distances are not equal.
To calculate the intensity for the green dot, we will first proceed with a linear interpolation in X direction and calculate intensity values for blue pixels R1 and R2, see Equation 1 and Equation 2.
<math> f(R_1) \sim \frac{x_2-x}{x_2 - x_1} f(Q_11) + \frac{x-x_1}{x_2 - x_1}f(Q_{21}), where R_1 = (x, y_1) </math>
<math> f(R_2) \sim \frac{x_2-x}{x_2 - x_1} f(Q_{12}) + \frac{x-x_1}{x_2 - x_1}f(Q_{22}), where R_2 = (x, y_2) </math>
Then, we will do interpolation in Y direction, see Equation 3.
<math> f(P) \sim \frac{y_2-y}{y_2 - y_1} f(R_1) + \frac{y-y_1}{y_2 - y_1}f(R_2) </math>
This gives us the desired interpolated value for the point <math>P=f(x,y)</math>, see Equation 4.
<math> f(x,y) \sim \frac{f(Q_{11})}{(x_2-x_1)(y_2 - y_1)}(x_2 - x)(y_2 - y) + \frac{f(Q_{21})}{(x_2-x_1)(y_2 - y_1)} (x - x_1) (y_2 - y) + \frac{f(Q_{12})}{(x_2-x_1)(y_2 - y_1)} (x_2 - x) (y - y_1) + \frac{f(Q_{22})}{(x_2-x_1)(y_2 - y_1)} (x - x_1)(y - y_1) </math>
Trilinear Interpolation
Trilinear interpolation computes intensity values for voxels with unknown intensity values, which are located between known voxel values. It does it by linearly weighting the eight closest neighboring values.
Where to use
Trilinear interpolation is the default resampling interpolation method used in MIPAV registration techniques. In practice, a trilinear interpolation is identical to three successive linear interpolations, or two bilinear interpolations combined with a linear interpolation.
Example
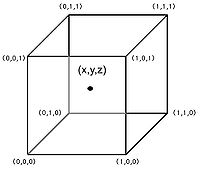
The figure on your right depicts the situation where it is desired to determine an intensity value at the point labeled (x, y, z), given the values at the corner of the cube. The unknown value is computed by combining the known corner values weight by their distance from the location of the point (x, y, z) according to the following formula:
<math>V_{xyz}</math> = <math>V_{000}</math> (1 - x) (1 - y) (1 - z) + <math>V_{100}</math> x (1 - y) (1 - z) + <math>V_{010}</math> (1 - x) y (1 - z) + <math>V_{001}</math> (1 - x) (1 - y) z + <math>V_{101}</math> x (1 - y) z + <math>V_{011}</math> (1 - x) y z + <math>V_{110}</math> x y (1 - z) + <math>V_{111}</math> x y z
B-spline basis interpolations
B-spline interpolation utilizes weighted voxel values in a larger neighborhood compared to trilinear interpolation. The larger number of values are weighted based on a 3-rd and 4-th order of polynomial, instead of a second order polynomial as in the case of trilinear interpolation. B-spline interpolation refers to the locations of the neighboring points as control points and combines the intensity values at these locations using a set of polynomial basis according to Equation 1.
The equation for k-order B-spline with n+1 control points (P0, P1, ... , Pn) is as follows:
<math> P(t) = \sum_{i=1}^{n+1} N_{i,k} (t) P_i, t_{min} \leq t < t_{max} </math>
In Equation 1, <math>N_{i,k}</math> are the polynomial functions of degree k-1, and n is the number of control points. Note, that the degree of the weighting polynomial is independent of the number of control points, n.
The weighting polynomial is recursively defined as
<math> N_{i,1} (t) = \left\{ \begin{array}{l l}
1 & \quad t_{i} \leq t < t_{i+1}\\
0 & \quad otherwize\\
\end{array} \right.
</math>
See also: Optimized automatic registration 3D