Correcting image spacing

A similarity or cost function measures the similarity between two images. During the registration the adjusted image V is transformed using the various transformation functions. And the similarity S(U;Vt) between the reference image U and transformed image Vt is then calculated.

Note: in MIPAV, we use the term cost function to refer to the negative cost function. That means that we assume that the transformation that gives the smallest value of the chosen inverse cost function is the transformation that also gives the best alignment.

Background

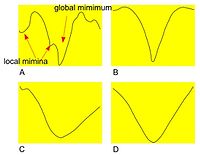
The plots of the Correlation Ratio cost function versus some of the individual parameter values. In each plot (A, B, C, and D), a single parameter is varied while the other are kept constant

For the registration algorithms, such as OAR, the main approach for determining an optimal transformation is to

1. Calculate a cost function,
2. Determine how it changes as individual transformation parameters are varied,
3. And find the parameters that minimize the value of the cost function.

The following figure (right) shows a plot of a sample cost function for a selection of transformation parameters.

The cost functions implemented in MIPAV:

• Correlation ratio
• Laplacian Zero Crossing
• Gradient Magnitude
• Least Squares
• Normalized Cross Correlation
• Normalized Mutual Information

Powell algorithm

In MIPAV, most of the methods and algorithms use the Powell algorithm to find the global minimum of the chosen cost function. For more information about the Powell algorithm, refer to http://math.fullerton.edu/mathews/n2003/PowellMethodMod.htm.

Correlation Ratio

Given two images I and R, the basic principle of the Correlation Ratio method is to search for a spatial transformation T and an intensity mapping f such that, by displacing R and remapping its intensities, the resulting image f(R* T) be as similar as possible to I. This could be achieved by minimizing the following correlation ratio function:

$min(T,f)of\displaystyle \sum \limits _{k}{I(x_{k})-f(R(T(x_{k})))}$

which integrates over the voxel positions $x_{k}$ in the image I.

Image types

Correlation Ratio can be used in multimodal image registration of Magnetic Resonance (MR), Computed Tomography (CT), and Positron Emission Tomography (PET) images.

Laplacian Zero-Crossing

The laplacian zero-crossing is a binary edge feature used for edge detection, see also Edge Detection: Zero X Laplacian algorithm. Convolution of an image with a laplacian kernel approximates the 2-nd partial derivative of the image. The laplacian zero-crossing corresponds to points of maximal (or minimal) gradient magnitude. Thus, laplacian zero-crossings represent "good" edge properties and should, therefore, have a low local cost meaning edge detection. If IL(q) is the laplacian of an image I at pixel q, then,

${\begin{cases}f_{Z}(q)=0;ifI_{L}(q)=0\\f_{Z}(q)=1;ifI_{L}(q)\neq 0\end{cases}}$

Though, application of a discrete laplacian kernel to a digital image produces very few zero-valued pixels. Rather, a zero-crossing is represented by two neighboring pixels that change from positive to negative values. Of these two neighboring pixels, the one closest to zero is used to represent the zero-crossing. The resulting feature cost contains single-pixel wide cost "canyons" used for boundary localization.

Gradient Magnitude

Gradient Magnitude provides a direct correlation between the edge strength and local cost. If $I_{x}$ and $I_{y}$ represent the partials of an image I in X and Y directions respectively, then the gradient magnitude G is approximated with the following formula:

$G={\sqrt {I_{x}^{2}+I_{y}^{2}}}$

The gradient is then scaled and inverted, so high gradients produce low costs and vice-versa. Thus, the gradient component function is

$f_{G}={\frac {max(G)-G}{max(G)}}=1-{\frac {G}{max(G)}}$

Finally, gradient magnitude costs can be scaled by Euclidean distance. To keep the resulting maximum gradient at unity, $f_{G}(q)$ can be scaled by 1, if q is a diagonal neighbor to p and by ${\frac {1}{\sqrt {2}}}$, if q is a horizontal or vertical neighbor.

Least Squares

Least squares measures the average of the squared difference in image intensities.

${\frac {\sum _{i=1}^{N}\{R(p_{i})-I(p_{i})\}^{2}}{N}}$

Where,

• R(p_i) = reference image(p_i) - minimum reference image value
• I(p_i) = input image(p_i) - minimum input image value
• N = the number of values over which the sum is performed

It can be divided by count to normalize the cost function or make it invariant to the number of voxels in the region of overlap. If two images show large differences in image intensity, then we recommend using Scaled Least Squares with a global scaling term added:

${\frac {\sum _{i=1}^{N}\{R(p_{i})-s*I(p_{i})\}^{2}}{N}}$

Image types

It can be shown that Least Squares is the optimum cost function when two images only differ by Gaussian noise. Images in two different modalities, such as PET and MRI, will never differ by only Gaussian noise. Even two images in the same modality, such as two PET images, will seldom only differ by Gaussian noise as medical scan noise is frequently not Gaussian and because the object often changes between the image acquisitions. The effectiveness of this cost function will be greatly diminished by small numbers of voxels having large intensity differences.

Normalized Cross Correlation

The Cross-Correlation function can be defined as

$CrossCorr(s,t)=\sum _{x}\sum _{y}R(x,y)I(x-s,y-t)$

Where,

• R-reference image intensity
• I-input image intensity

The summation is taken over the region (s,t) where R and I overlap. For any value of (s,t) inside R(x,y) the cross-correlation function yields one value of CrossCorr. The maximum value of CrossCorr(s,t) indicates the position where I(x,y) best matches R(x,y).

Normalized Cross Correlation is 0 for identical images and approaches 1 for images that are very different.

Image types

The Cross-Correlation function can be used for aligning the images that have a linear relationship between the intensity values in the images. E.g. images acquired using the same modality. However, the Normalized Cross-Correlation may not work very well in two images that are identical except for a global scaling factor.

Normalized Mutual Information

Mutual information (MI) measures how well one image explains the other. In medical image processing, MI is often used as

• a similarity measure for image registration for images that were acquired at different times or by different modalities and
• for combining multiple images to build 3D models.

The mutual information of random variables A and B is defined as:

$MI(A,B)=\sum _{ab}p(a,b)log{\frac {p(a,b)}{p(a)p(b)}}$

Where, p(a,b) is the joint probability distribution function of A and B, and p(a) and p(b) are the marginal probability distribution functions of A and B respectively.

MI could also be defined as MI(A,B) = H(A) + H(B)-H(A,B),

Where H(A) and H(B) are the Shannon entropy of image A and B respectively, computed based on the probability distributions of their grey values. And H(A,B) denotes the conditional entropy, which is based on the conditional probabilities p(a |b) - the chance of grey value a in image A given that the corresponding voxel in B has grey value b. MI measures the distance between the joint distributions of the images' gray values p(a,b) and the distribution when assume that images are independent from each other.

Normalized mutual information

Normalized mutual information can be calculated as normalized MI, where $NMI(A,B)=(H(A)+H(B))/H(A,B)$.

Image types

The normalized mutual information has been shown to work very well for registering multi-modality images and also time series images. In MIPAV the normalized mutual information approaches 0 for identical images and approaches 1 for images that are very different.

References

Bjorn Hamre "Three-dimensional image registration of magnetic resonance (MRI) head volumes" Section for Medical Image Analysis and Informatics Department of Physiology & Department of Informatics University of Bergen, Norway.

Woods R.P., Handbook of Medical Image Processing and Analysis, Chapter 33 "Within-Modality Registration Using Intensity-Based Cost Functions", Editor, Isaac N. Bankman, Academic Press, 2000, pp. 529-553.

Mortensen E., Barrett W., "Intelligent scissors for image composition", International Conference on Computer Graphics and Interactive Techniques archive. Proceedings of the 22-nd annual conference on Computer graphics and interactive techniques, pp. 191 - 198, 1995, ISBN:0-89791-701-4.

Josien P. W. Pluim, J. B. Antoine Maintz and Max A. Viergever. Mutual information based registration of medical images: a survey. IEEE TRANSACTIONS ON MEDICAL IMAGING, VOL. XX, NO. Y, MONTH 2003.

Powell method to find the global minimum: mathews/n2003/PowellMethodMod.html http://math.fullerton.edu/ mathews/n2003/PowellMethodMod.html

See also

• MIPAV WIKI
• Using MIPAV Algorithms
• Degrees of freedom