BSpline registration: Detecting folding and Background: Difference between pages
m (1 revision imported) |
MIPAV>Angelfish100 No edit summary |
||
| Line 1: | Line 1: | ||
'''In this section . . .<br />''' | |||
*Background<br /> | |||
*References <br /> | |||
Designed specifically for medical researchers, MIPAV concentrates on providing those researchers with the tools needed to do their work. It reads image files of many different formats and allows images to be displayed and measured using the most meaningful method to achieve research goals. MIPAV's flexibility becomes apparent when its capabilities are expanded and fine tuned through the development of plug-in programs that tailor solutions to meet specific requirements.<br /> | |||
Using MIPAV to display, label, and measure brain components in Talairach space demonstrates both: MIPAV's native ability to display and measure brain images in Talairach space and the tailoring provided through the Talairach Transformation wizard and the FANTASM (Fuzzy and Noise Tolerant Adaptive Segmentation Method) plug-in programs, developed by the Johns Hopkins University. | |||
== Background == | |||
In 1988 Jean Talairach and Pierre Tournoux developed a three-dimensional proportional grid system that can be used to identify and measure brains from any number of patients despite the variability of brain sizes and proportions. The premise of the system is that brain components that cannot be seen or identified can be defined in relation to other anatomic cerebral structures. In the Talairach system, the anterior commissure (AC) and posterior commissure (PC) are the structures from which the system of reference is developed.<br /> | |||
The Talairach system establishes the maximal dimensions of the brain in three planes of space: <span style="font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline">''<font color="#000000">x, y</font>''</span> and <span style="font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline">''<font color="#000000">z</font>''</span><nowiki>: </nowiki> | |||
<div style="font-style: normal; font-weight: normal; margin-bottom: 0pt; margin-left: 24pt; margin-right: 0pt; margin-top: 5pt; text-align: left; text-decoration: none; text-indent: -24pt; text-transform: none; vertical-align: baseline"><font color="#000000"> <span style="font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline">''<font color="#000000">AC-PC line (X axis)</font>''</span>-A horizontal line running through the anterior and posterior commissures. <br /></font></div><div style="font-style: normal; font-weight: normal; margin-bottom: 0pt; margin-left: 24pt; margin-right: 0pt; margin-top: 5pt; text-align: left; text-decoration: none; text-indent: -24pt; text-transform: none; vertical-align: baseline"><font color="#000000"> <span style="font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline">''<font color="#000000">VCA line (verticofrontal line, or Y axis)</font>''</span>-A vertical line passing through the anterior commissure<br /></font></div><div style="font-style: normal; font-weight: normal; margin-bottom: 0pt; margin-left: 24pt; margin-right: 0pt; margin-top: 5pt; text-align: left; text-decoration: none; text-indent: -24pt; text-transform: none; vertical-align: baseline"><font color="#000000"> <span style="font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline">''<font color="#000000">Midline (Z axis)</font>''</span>-A line forming the interhemispheric sagittal plane<br /></font></div> | |||
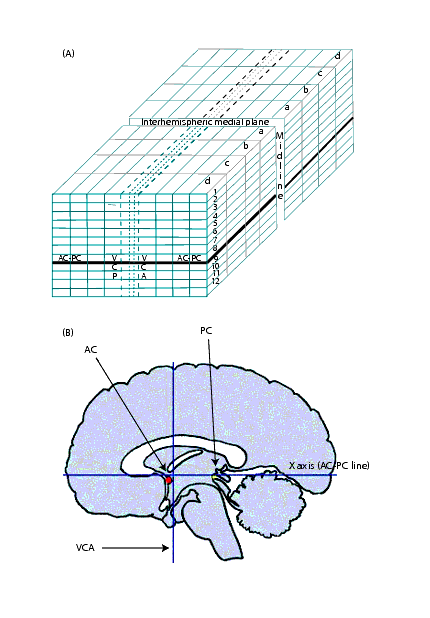
Often referred to as the "origin," the anterior commissure is commonly used to describe structures. For example, a structure is described as "AC 13 mm" for the frontal lobe or "AC - 35 mm" for the occipital pole. These descriptions assume that the anterior commissure is in the positive direction. However, the Talairach system does not use positive and negative directions. Instead, it labels quadrants according to number and letters ([TechGuide_Background.html#1005540 Figure 15]A). The AC-PC line defines the horizontal plane, the VCA line defines the vertical plane, and the midline defines the depth plane. Because the anterior commissure and posterior commissure do not occur in the same axial slice, reslicing is necessary to put the brain into Talairach space. | |||
= | {| align="left" | ||
| | |||
[[Image:TechGuide_Backgrounda.gif]] | |||
|} | |||
<br clear="all" />Jean Talairach and Pierre Tournoux, <span style="font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline">''<font color="#000000">Co-Planar Stereotaxic Atlas of the Human Brain</font>''</span>, Thieme Medical Publishers, New York, 1988.<br /> | |||
This technical guide explains how to install and use two MIPAV plug-in programs-the Talairach Transformation wizard and FANTASM to: | |||
<div style="font-style: normal; font-weight: normal; margin-bottom: 0pt; margin-left: 24pt; margin-right: 0pt; margin-top: 5pt; text-align: left; text-decoration: none; text-indent: -24pt; text-transform: none; vertical-align: baseline"><font color="#000000"> Create the <span style="font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline">''<font color="#000000">x, y,</font>''</span> and <span style="font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline">''<font color="#000000">z</font>''</span> planes of space in an image of a brain<br /></font></div><div style="font-style: normal; font-weight: normal; margin-bottom: 0pt; margin-left: 24pt; margin-right: 0pt; margin-top: 5pt; text-align: left; text-decoration: none; text-indent: -24pt; text-transform: none; vertical-align: baseline"><font color="#000000"> Transfer Talairach labels to an image of a brain<br /></font></div><div style="font-style: normal; font-weight: normal; margin-bottom: 0pt; margin-left: 24pt; margin-right: 0pt; margin-top: 5pt; text-align: left; text-decoration: none; text-indent: -24pt; text-transform: none; vertical-align: baseline"><font color="#000000"> Measure brain components in Talairach space<br /></font></div><div style="font-style: normal; font-weight: normal; margin-bottom: 0pt; margin-left: 0pt; margin-right: 0pt; margin-top: 0pt; text-align: left; text-decoration: none; text-indent: 0pt; text-transform: none; vertical-align: baseline"><font color="#000000"> <br /></font></div><div style="font-style: normal; font-weight: normal; margin-bottom: 0pt; margin-left: 0pt; margin-right: 0pt; margin-top: 0pt; text-align: left; text-decoration: none; text-indent: 0pt; text-transform: none; vertical-align: baseline"><font color="#000000"> | |||
{| border="1" cellpadding="5" | |||
|+ <div style="font-style: normal; margin-bottom: 3pt; margin-left: 0pt; margin-right: 0pt; margin-top: 9pt; text-align: left; text-decoration: none; text-indent: 0pt; text-transform: none; vertical-align: baseline">'''<font color="#000000"> Figure 15. Talairach space: (A) Quadrants labeled by number and letters and (B) horizontal, vertical, and depth planes<br /></font>'''</div> | |||
|- | |||
| | |||
[[Image:exampleTalairachCubeBrain.gif]] | |||
|} | |||
=== Talairach Transformation wizard === | |||
The Talairach Transformation wizard is a plug-in program for MIPAV that performs a semimanual transformation of image datasets of the brain to Talairach (stereotaxic) coordinates, providing atlas-based labeling. The Talairach coordinates allow researchers to easily identify subregions of the brain and measure their volume. It includes labels for 148 different substructures of the brain at various scales, obtained from the <span style="font-style: normal; font-weight: normal; text-transform: none; vertical-align: baseline"><u><font color="#000000">[ http://ric.uthscsa.edu/projects/talairachdaemon.html ]</font></u></span><span style="font-style: normal; font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline"><font color="#000000">Talairach Daemon database</font></span>, along with a set of volumetric images of the labels.<br /></font></div> | |||
< | === FANTASM === | ||
The FANTASM plug-in program<span style="font-style: normal; font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline"><font color="#000000"> is a different version of the Fuzzy C-mean algorithm for segmenting 2D and 3D images. It incorporates a spatial constraint that requires neighboring pixels to be similar and reduces the noise effect obtained with the Fuzzy C-mean algorithm. It can deal with outliers. Plans for a future version of FANTASM incorporates inhomogeneity correction. </font></span><br /> | |||
== References == | |||
ICBM atlas created by the International Consortium on Brain Mapping (ICBM), automatic <br />(<span style="font-style: normal; font-weight: normal; text-transform: none; vertical-align: baseline"><u><font color="#000000">http://www.loni.ucla.edu/ICBM/ICBM_BrainTemplate.html</font></u></span>).<br /> | |||
<div style="font-style: normal; font-weight: normal; margin-bottom: 4pt; margin-left: 0pt; margin-right: 0pt; margin-top: 11pt; text-align: left; text-decoration: none; text-indent: 0pt; text-transform: none; vertical-align: baseline"><font color="#000000"> Jean Talairach and Pierre Tournoux, <span style="font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline">''<font color="#000000">Co-Planar Stereotaxic Atlas of the Human Brain</font>''</span>, Thieme Medical Publishers, New York, 1988. <br /></font></div><div style="font-style: normal; font-weight: normal; margin-bottom: 4pt; margin-left: 0pt; margin-right: 0pt; margin-top: 11pt; text-align: left; text-decoration: none; text-indent: 0pt; text-transform: none; vertical-align: baseline"><font color="#000000"> Neva Chernizasky, <span style="font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline">''<font color="#000000">Medical Imaging: Orientation</font>''</span>, Paper prepared for Matthew McAuliiffe, Ph.D. Center for Information Technology, National Institutes of Health, August 31, 2001.<br /></font></div><div style="font-style: normal; font-weight: normal; margin-bottom: 4pt; margin-left: 0pt; margin-right: 0pt; margin-top: 11pt; text-align: left; text-decoration: none; text-indent: 0pt; text-transform: none; vertical-align: baseline"><font color="#000000"> Dzung L. Pham, "Spatial Models for Fuzzy Clustering," <span style="font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline">''<font color="#000000">Computer Vision and Image Understanding</font>''</span>, vol. 84, pp. 285-297, 2001.<br /></font></div><div style="font-style: normal; font-weight: normal; margin-bottom: 4pt; margin-left: 0pt; margin-right: 0pt; margin-top: 11pt; text-align: left; text-decoration: none; text-indent: 0pt; text-transform: none; vertical-align: baseline"><font color="#000000"> Pierre-Louis Bazin, Dzung L. Pham, William Gandler, and Matthew McAuliffe. "Free Software Tools for Atlas-based Volumetric Neuroimage Analysis," to be published in the <span style="font-weight: normal; text-decoration: none; text-transform: none; vertical-align: baseline">''<font color="#000000">Proceedings of the SPIE Medical Image 2005 Conference</font>''</span>, The International Society for Optical Engineering (SPIE), Bellingham, Washington, 2005.<br /></font></div> | |||
<div><div align=" | |||
< | |||
< | |||
= | |||
Revision as of 16:39, 7 March 2012
In this section . . .
- Background
- References
Designed specifically for medical researchers, MIPAV concentrates on providing those researchers with the tools needed to do their work. It reads image files of many different formats and allows images to be displayed and measured using the most meaningful method to achieve research goals. MIPAV's flexibility becomes apparent when its capabilities are expanded and fine tuned through the development of plug-in programs that tailor solutions to meet specific requirements.
Using MIPAV to display, label, and measure brain components in Talairach space demonstrates both: MIPAV's native ability to display and measure brain images in Talairach space and the tailoring provided through the Talairach Transformation wizard and the FANTASM (Fuzzy and Noise Tolerant Adaptive Segmentation Method) plug-in programs, developed by the Johns Hopkins University.
Background
In 1988 Jean Talairach and Pierre Tournoux developed a three-dimensional proportional grid system that can be used to identify and measure brains from any number of patients despite the variability of brain sizes and proportions. The premise of the system is that brain components that cannot be seen or identified can be defined in relation to other anatomic cerebral structures. In the Talairach system, the anterior commissure (AC) and posterior commissure (PC) are the structures from which the system of reference is developed.
The Talairach system establishes the maximal dimensions of the brain in three planes of space: x, y and z:
Often referred to as the "origin," the anterior commissure is commonly used to describe structures. For example, a structure is described as "AC 13 mm" for the frontal lobe or "AC - 35 mm" for the occipital pole. These descriptions assume that the anterior commissure is in the positive direction. However, the Talairach system does not use positive and negative directions. Instead, it labels quadrants according to number and letters ([TechGuide_Background.html#1005540 Figure 15]A). The AC-PC line defines the horizontal plane, the VCA line defines the vertical plane, and the midline defines the depth plane. Because the anterior commissure and posterior commissure do not occur in the same axial slice, reslicing is necessary to put the brain into Talairach space.
Jean Talairach and Pierre Tournoux, Co-Planar Stereotaxic Atlas of the Human Brain, Thieme Medical Publishers, New York, 1988.
This technical guide explains how to install and use two MIPAV plug-in programs-the Talairach Transformation wizard and FANTASM to:
Talairach Transformation wizard
The Talairach Transformation wizard is a plug-in program for MIPAV that performs a semimanual transformation of image datasets of the brain to Talairach (stereotaxic) coordinates, providing atlas-based labeling. The Talairach coordinates allow researchers to easily identify subregions of the brain and measure their volume. It includes labels for 148 different substructures of the brain at various scales, obtained from the [ http://ric.uthscsa.edu/projects/talairachdaemon.html ]Talairach Daemon database, along with a set of volumetric images of the labels.FANTASM
The FANTASM plug-in program is a different version of the Fuzzy C-mean algorithm for segmenting 2D and 3D images. It incorporates a spatial constraint that requires neighboring pixels to be similar and reduces the noise effect obtained with the Fuzzy C-mean algorithm. It can deal with outliers. Plans for a future version of FANTASM incorporates inhomogeneity correction.
References
ICBM atlas created by the International Consortium on Brain Mapping (ICBM), automatic
(http://www.loni.ucla.edu/ICBM/ICBM_BrainTemplate.html).