Filters (Spatial): Regularized Isotropic (Nonlinear) Diffusion and Filters (Spatial): Slice Averaging: Difference between pages

From MIPAV
(Difference between pages)
Jump to navigation Jump to search
m (1 revision imported)
 
MIPAV>Olga Vovk
mNo edit summary
 
Line 1: Line 1:
Regularized isotropic nonlinear diffusion is a specific technique within the general classification of diffusion filtering. Diffusion filtering, which models the diffusion process, is an iterative approach of spatial filtering in which image intensities in a neighborhood are utilized to compute new intensity values.
''This algorithm provides a way of reducing image noise by summing together a set of noisy images and dividing the sum by the number of images. The algorithm assumes that the noise in the images is uncorrelated and has zero average value.''
------


== Background ==
{| width="90%" border="1" frame="hsides" frame="hsides"
Two major advantages of diffusion filtering over many other spatial domain filtering algorithms are:
|-
 
| width="9%" valign="top" |
* ''A priori'' image information can be incorporated into the filtering process;
[[Image:noteicon.gif]]
* The iterative nature of diffusion filtering allows for fine-grain control over the amount of filtering performed.
| width="81%" bgcolor="#B0E0E6" |
[http://mipav.cit.nih.gov/documentation/HTML Algorithms/FiltersSpatialSliceAveraging.html For more information about the algorithm, refer to the MIPAV web site: {http://mipav.cit.nih.gov/documentation/HTML Algorithms/FiltersSpatialSliceAveraging.html}. ]
|}


There is not a consistent naming convention in the literature to identify different types of diffusion filters. This documentation follows the approach used by  Weickert [http://www.mia.uni-saarland.de/weickert/demos.html]. Specifically, since the diffusion process relates a concentration gradient with a flux, ''isotropic diffusion'' means that these quantities are parallel. ''Regularized'' means that the image is filtered prior to computing the derivatives required during the diffusion process. In linear diffusion the filter coefficients remain constant throughout the image, while ''nonlinear'' diffusion means the filter coefficients change in response to differential structures within the image.
<br />


== Image types ==
== Image types ==


You can apply this algorithm to all data types except complex and to 2D, 2.5D, and 3D images.
You can apply this algorithm to all image data types and to 2D, 2.5D, and 3D images.


== Applying Regularized Isotropic (Nonlinear) Diffusion ==
== Applying the Slice Averaging algorithm ==


To run this algorithm, complete the following steps:
To run this algorithm, complete the following steps:


# Select Algorithms &gt; Filter &gt; Regularized Isotropic Diffusion. The Regularized Isotropic Diffusion dialog box opens (Figure 1).
# Open an image.
# Complete the fields in the dialog box.
# Select Algorithms &gt; Filter (spatial) &gt; Slice Averaging. The Slice Averaging dialog box (Figure 1) opens.
# When complete, click OK.


; The algorithm begins to run, and a status window appears. When the algorithm finishes, the resulting image appears in a new image window.
<div>
 
<div><br /> </div><div>


{| border="1" cellpadding="5"
{| border="1" cellpadding="5"
|+ <div>'''Figure 1. Regularized Isotropic Diffusion dialog box  ''' </div>
|+ <div>'''Figure 1. Slice Averaging dialog box''' </div>
|-
|-
|
|
<div>'''Number of iterations''' </div>
<div>'''3''' </div>
|
|
<div>Specifies the number of iterations, or number of times, to apply the algorithm to the image. </div>
<div>Averages 3 slices in the dataset and creates a 3D image. </div>
| rowspan="4" colspan="1" |
| rowspan="7" colspan="1" |
<div><div><center>[[Image:dialogboxRegularizedIsotropicDiffusion.jpg]]</center></div> </div>
<div><div><center>[[Image:dialogboxSliceAveraging.jpg]]</center></div> </div>
|-
|-
|
|
<div>'''Gaussian standard deviation''' </div>
<div>'''5''' </div>
|
|
<div>Specifies the standard deviation of the Gaussian filter used to regularize the image. </div>
<div>Averages 5 slices in the dataset and creates a 3D image. </div>
|-
|-
|
|
<div>'''Diffusion contrast parameter''' </div>
<div>'''7''' </div>
|
|
<div>Specifies the inflection point in the diffusivity function, which dictates the shape of the function. </div>
<div>Averages 7 slices in the dataset and creates a 3D image. </div>
|-
|-
|
|
<div>'''Process each slice separately''' </div>
<div>'''All''' </div>
|
|
<div>Applies the algorithm to each slice individually. By default, this option is selected. </div>
<div>Averages all of the slices in the dataset and creates a 2D image (default choice). </div>
|-
|
<div>'''New image''' </div>
|
<div>Shows the results of the algorithm in a new image window (default choice). </div>
|-
|
<div>'''Replace image''' </div>
|
<div>Replaces the current active image with the newly calculated <br />image. </div>
|-
|-
|
|
<div>'''OK''' </div>
<div>'''OK''' </div>
| rowspan="1" colspan="2" |
|
<div>Applies the algorithm according to the specifications in this dialog box.  </div>
<div>Applies the algorithm according to the specifications in this dialog box.  </div>
|-
|-
Line 66: Line 76:
|}
|}


== See also: ==
</div>
**[[Filters (Spatial): Adaptive Noise Reduction]]
 
**[[Filters (Frequency)]]
# Complete the information in the dialog box.
**[[Filters (Spatial): Adaptive Path Smooth]]
# Click OK.
**[[Filters (Spatial) Anisotropic Diffusion]]
**[[Filters (Spatial): Coherence-Enhancing Diffusion]]
**[[Filters (Spatial): Gaussian Blur]]
**[[Filters (Spatial): Gradient Magnitude]]
**[[Filters (Spatial): Haralick Texture]]
**[[Filters (Spatial) Laplacian]]
**[[Filters (Spatial): Local Normalization]]
**[[Filters (Spatial): Mean]]
**[[Filters (Spatial): Median]]
**[[Filters (Spatial): Mode]]
**[[Filters (Spatial): Nonmaximum Suppression]]
**[[Filters (Spatial): Nonlinear Noise Reduction|Nonlinear Noise Reduction]]
**[[Filters (Spatial): Slice Averaging]]


; The algorithms begins to run, and a pop-up window appears with the status. The following messages appear: "Averaging data" and "Importing average data."
; When the algorithm finishes running, the pop-up window closes, and the results appear either in a new window or replace the image in which the algorithm was applied.


[[Category:Help]]
[[Category:Help]]
[[Category:Help:Algorithms]]
[[Category:Help:Algorithms]]

Revision as of 18:43, 27 July 2012

This algorithm provides a way of reducing image noise by summing together a set of noisy images and dividing the sum by the number of images. The algorithm assumes that the noise in the images is uncorrelated and has zero average value.

Noteicon.gif

Algorithms/FiltersSpatialSliceAveraging.html For more information about the algorithm, refer to the MIPAV web site: {http://mipav.cit.nih.gov/documentation/HTML Algorithms/FiltersSpatialSliceAveraging.html}.


Image types

You can apply this algorithm to all image data types and to 2D, 2.5D, and 3D images.

Applying the Slice Averaging algorithm

To run this algorithm, complete the following steps:

  1. Open an image.
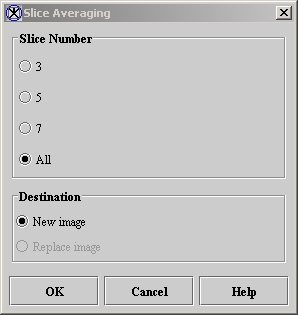
  2. Select Algorithms > Filter (spatial) > Slice Averaging. The Slice Averaging dialog box (Figure 1) opens.
Figure 1. Slice Averaging dialog box
3
Averages 3 slices in the dataset and creates a 3D image.
DialogboxSliceAveraging.jpg
5
Averages 5 slices in the dataset and creates a 3D image.
7
Averages 7 slices in the dataset and creates a 3D image.
All
Averages all of the slices in the dataset and creates a 2D image (default choice).
New image
Shows the results of the algorithm in a new image window (default choice).
Replace image
Replaces the current active image with the newly calculated
image.
OK
Applies the algorithm according to the specifications in this dialog box.
Cancel
Disregards any changes that you made in this dialog box and closes the dialog box.
Help
Displays online help for this dialog box.
  1. Complete the information in the dialog box.
  2. Click OK.
The algorithms begins to run, and a pop-up window appears with the status. The following messages appear
"Averaging data" and "Importing average data."
When the algorithm finishes running, the pop-up window closes, and the results appear either in a new window or replace the image in which the algorithm was applied.
Retrieved from "https://mipav.cit.nih.gov/pubwiki/index.php?title=Filters_(Spatial):_Regularized_Isotropic_(Nonlinear)_Diffusion&oldid=211"