Filters (Spatial): Gaussian Blur and Filters (Spatial): Gradient Magnitude: Difference between pages

From MIPAV
(Difference between pages)
Jump to navigation Jump to search
m (1 revision imported)
 
MIPAV>Olgavovk
mNo edit summary
 
Line 1: Line 1:
This algorithm blurs an image or the VOI of the image with a Gaussian function at a user-defined scale sigma (standard deviation [SD]). In essence, convolving a Gaussian function produces a similar result to applying a low-pass or smoothing filter. A'' low-pass filter'' attenuates high-frequency components of the image (i.e., edges) and passes low-frequency components. This results in the blurring of the image. ''Smoothing filters'' are typically used for noise reduction and for blurring. The standard deviation of the Gaussian function controls the amount of blurring. A large standard deviation (i.e., > 2) significantly blurs, while a small standard deviation (i.e., 0.5) blurs less. If the objective is to achieve noise reduction, a rank filter (median) might be more useful in some circumstances.
Edge detection is the identification of meaningful discontinuities in gray level or color images. Edges are formed between two regions that have differing intensity values. This algorithm calculates the gradient magnitude of an image (or VOI of the image) using the first derivatives (''Gx'', ''Gy'', and ''Gz'' [3D] ) of the Gaussian function at a user-defined scale sigma (standard deviation, or SD) and convolving it with image. The convolution of the first derivatives of the Gaussian with an image is a robust method of extracting edge information. By varying the SD, a scale-space of edges can easily be constructed.
 
Advantages to convolving the Gaussian function to blur an image include:
 
* Structure is not added to the image.
* It, as well as the Fourier Transform of the Gaussian, can be analytically calculated.
* By varying the SD, a Gaussian scale space can easily be constructed.
 
=== Background ===
 
The radially symmetric Gaussian, in an ''n''-dimensional space, is:''''
 
Equation 10 <div align "left"> </div><br />
 
[[File:FiltersSpatialGaussianBlur5.jpg]]
 
where [[Image:FiltersSpatialGaussianBlur6.jpg]] (referred to as the ''scale''), is the standard deviation of the Gaussian and is a free parameter that describes the width of the operator (and thus the degree of blurring) and ''n'' indicates the number of dimensions.
 
Geometric measurements of images can be obtained by spatially convolving (shift-invariant and linear operation) a Gaussian neighborhood operator with an image, ''I'', where [[Image:FiltersSpatialGaussianBlur7.jpg]] represents an ''n''-dimensional image. The convolution process produces a weighted average of a local neighborhood where the width of the neighborhood is a function of the scale of the Gaussian operator. The scale of the Gaussian controls the resolution of the resultant image and thus the size of the structures that can be measured. A scale-space for an image [[Image:FiltersSpatialGaussianBlur8.jpg]]of increasingly blurred images can be defined by L:nx''[[Image:FiltersSpatialGaussianBlur9.jpg]] [[Image:FiltersSpatialGaussianBlur10.jpg]]'' and ''[[Image:FiltersSpatialGaussianBlur11.jpg]]'' where [[Image:xcirclenm.jpg]] represents convolution.
 
The following is the calculation of the full-width half max (FWHM) of the Gaussian function.
 
<div>
 
{| border="1" cellpadding="5"
|+
|-
|
<math>
G(x, \sigma) = \frac {1}{\sqrt {2\pi\sigma^2}}e^{-\frac {x^2} {2\sigma^2}}
</math>
 
<math>
ln 0.5 \frac {1}{\sqrt {2\pi \sigma^2}} = ln \left ( \frac {1}{\sqrt {2\pi\sigma^2}}e^{-\frac {x^2} {2\sigma^2}} \right )
</math>
 
<math>
ln0.5 + ln \left ( \frac {1}{\sqrt {2\pi\sigma^2}} \right ) =ln \left ( \frac {1}{\sqrt {2\pi\sigma^2}} \right ) + ln \left (e^{-\frac {x^2} {2\sigma^2}} \right )
</math>
 
<math>
-0.693 = - \frac {x^2} {2\sigma^2}
</math>
 
<math>
1.18\sigma = x
</math>
 
|}
 
 
Figure 2 shows the Gaussian function. The dotted lines indicate the standard deviation of 1. The FWHM is indicated by the solid lines. For a Gaussian with a standard deviation equal to 1 ([[Image:FiltersSpatialGaussianBlur13.jpg]]), the FWHM is 2.36.
 
<div>
 
{| border="1" cellpadding="5"
|+ <div>'''Figure 1. Gaussian Blur algorithm processing''' </div>
|-
|
<div><div align="left">[[Image:GaussianBlurProcessing2.jpg]]</div> </div>
|}
 
</div>
 
Figure 1 shows a Gaussian scale-space of the sagittal view of a MR head image. The original image is shown in the upper left ([[Image:FiltersSpatialGaussianBlur14.jpg]]). Varying ''s'' from 0.5 to 5.5 in steps of 0.5 blurs the other images (from left to right and top to bottom).
 
<div>
 
{| border="1" cellpadding="5"
|+ <div>'''Figure 2. Gaussian function''' </div>
|-
|
<div><div align="left">[[Image:GaussianFunction3.jpg]]</div> </div>
|}
 
</div>
 
Note that as the scale increases, small-scale features are suppressed. For example, at small scales the individual folds of the brain are quite defined, but, as the scale increases, these folds diffuse together resulting in the formation of a region one might define as the brain.


==== Image types ====
==== Image types ====


You can apply this algorithm to all image data types except Complex and to 2D, 2.5D, 3D, and 4D images.
You can apply this algorithm to all image data types except complex and to 2D, 2.5D, 3D, and 4D images.


* By default, the resultant image is a float type image.
==== Special notes ====
* By selecting Process each slide independently (2.5D) in the Gaussian Blur dialog box, you can achieve 2.5D blurring (each slice of the volume is blurred independently) of a 3D dataset (Figure 1).


==== Special notes ====
The following notes apply:


None.
* The resultant image is, by default, a float type image;
* To achieve 2.5D blurring (each slide of the volume is processed independently), select Process each slide independently (2.5D) in the Gradient Magnitude dialog box.


==== References ====
==== References ====


See the following references for more information about this algorithm:
Refer to the following references for more information:


J. J. Koenderink, "The Structure of Images," ''Biol Cybern'' 50:363-370, 1984.
Raphael C. Gonzalez and Richard E. Woods, ''Digital Image Processing'' (Boston: Addison-Wesley, 1992).


J. J. Koenderink and A. J. van Doorn, "Receptive Field Families," ''Biol Cybern'' 63:291-298, 1990.
J. J. Koenderink, "The Structure of Images," ''Biol Cybern'' 50: 363-370, 1984.


Tony Lindeberg, "Linear Scale-Space I: Basic Theory," ''Geometry-Driven Diffusion in Computer Vision'', Bart M. Ter Har Romeney, ed. (Dordrecht, The Netherlands: Kluwer Academic Publishers, 1994), pp. 1-38.
Tony Lindeberg, "Linear Scale-Space I: Basic Theory," ''Geometry-Driven Diffusion in Computer Vision'', Bart M. Ter Har Romeney, ed. (Dordrecht, The Netherlands: Kluwer Academic Publishers, 1994), pp. 1-38.


R. A. Young, "The Gaussian Derivative Model for Machine Vision: Visual Cortex Simulation," ''Journal of the Optical Society of America'', GMR-5323, 1986.
=== Applying the Gradient Magnitude algorithm ===
 
=== Applying the Gaussian Blur algorithm ===


To run this algorithm, complete the following steps:
To run this algorithm, complete the following steps:


# Select Algorithms &gt; Filter &gt; Gaussian Blur. The Gaussian Blur dialog box opens (Figure 3).
# Select Algorithms &gt; Filter &gt; Gradient Magnitude. The Gradient Magnitude dialog box opens (Figure 1).
# Complete the information in the dialog box.
# Complete the information in the dialog box.
# Click OK.
# When complete, click OK. The algorithm begins to run.
 
; A pop-up window appears with the status. The following message appears: "Calculating the Gradient Magnitude." When the algorithm finishes running, the pop-up window closes.
; Depending on whether you selected New Image or Replace Image, the result appears in a new window or replaces the image to which the algorithm was applied.
 
<div> </div><div>


; The algorithm begins to run, and a pop-up window appears with the status. The following message appears: "Blurring Image."
; When the algorithm finishes running, the pop-up window closes, and the results appear in either a new window or replace the image to which the algorithm was applied.
{| border="1" cellpadding="5"
{| border="1" cellpadding="5"
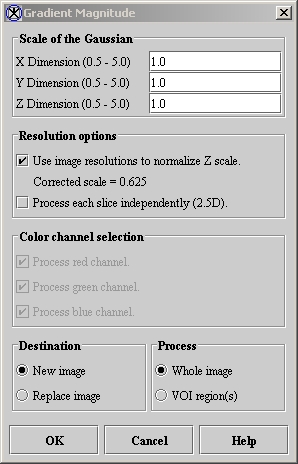
|+ <div>'''Figure 3. Gaussian Blur dialog box ''' </div>
|+ <div>'''Figure 1. Gradient Magnitude dialog box''' </div>
|-
|-
|
|
Line 119: Line 42:
|
|
<div>Indicates the standard deviation (SD) of Gaussian in the ''X'' direction. </div>
<div>Indicates the standard deviation (SD) of Gaussian in the ''X'' direction. </div>
| rowspan="8" colspan="1" |
| rowspan="7" colspan="1" |
<div><br /> </div><div><br /> </div><div><br /> </div><div><div align="left">[[Image:dialogboxGaussianBlur.jpg]]</div> </div><div><br /> </div><div><br /> </div><div><br /> </div><div><br /> </div><div><br /> </div><div><br /> </div><div><br /> </div><div><br /> </div><div><br /> </div><div><br /> </div><div><br /> </div><div><br /> </div><div><br /> </div>
<div><div><center>[[Image:dialogboxGradientMagnitude.jpg]]</center></div> </div><div> </div>
|-
|-
|
|
Line 140: Line 63:
<div>'''Process each slice independently (2.5D)''' </div>
<div>'''Process each slice independently (2.5D)''' </div>
|
|
<div>Blurs each slice of the dataset independently of adjacent slices. </div>
<div>Blurs each slice of the dataset independently. </div>
|-
|-
|
|
<div>'''Process red channel''' </div>
<div>'''Process red channel''' </div>
|
|
<div>Applies the algorithm to the red channel only. </div>
<div>Applies algorithm to the red channel only. </div>
|-
|-
|
|
<div>'''Process green channel''' </div>
<div>'''Process green channel''' </div>
|
|
<div>Applies the algorithm to the green channel only. </div>
<div>Applies algorithm to the green channel only. </div>
|-
|-
|
|
<div>'''Process blue channel''' </div>
<div>'''Process blue channel''' </div>
|
| rowspan="1" colspan="2" |
<div>Applies the algorithm to the blue channel only. </div>
<div>Applies algorithm to the blue channel only. </div>
|-
|-
|
|
Line 180: Line 103:
<div>'''OK''' </div>
<div>'''OK''' </div>
| rowspan="1" colspan="2" |
| rowspan="1" colspan="2" |
<div>Applies the algorithm according to the specifications in this dialog box.  </div>
<div>Applies the Gradient Magnitude algorithm according to the specifications in this dialog box.  </div>
|-
|-
|
|
Line 192: Line 115:
<div>Displays online help for this dialog box. </div>
<div>Displays online help for this dialog box. </div>
|}
|}
</div>


[[Category:Help]]
[[Category:Help]]
[[Category:Help:Algorithms]]
[[Category:Help:Algorithms]]

Revision as of 18:18, 18 May 2012

Edge detection is the identification of meaningful discontinuities in gray level or color images. Edges are formed between two regions that have differing intensity values. This algorithm calculates the gradient magnitude of an image (or VOI of the image) using the first derivatives (Gx, Gy, and Gz [3D] ) of the Gaussian function at a user-defined scale sigma (standard deviation, or SD) and convolving it with image. The convolution of the first derivatives of the Gaussian with an image is a robust method of extracting edge information. By varying the SD, a scale-space of edges can easily be constructed.

Image types

You can apply this algorithm to all image data types except complex and to 2D, 2.5D, 3D, and 4D images.

Special notes

The following notes apply:

  • The resultant image is, by default, a float type image;
  • To achieve 2.5D blurring (each slide of the volume is processed independently), select Process each slide independently (2.5D) in the Gradient Magnitude dialog box.

References

Refer to the following references for more information:

Raphael C. Gonzalez and Richard E. Woods, Digital Image Processing (Boston: Addison-Wesley, 1992).

J. J. Koenderink, "The Structure of Images," Biol Cybern 50: 363-370, 1984.

Tony Lindeberg, "Linear Scale-Space I: Basic Theory," Geometry-Driven Diffusion in Computer Vision, Bart M. Ter Har Romeney, ed. (Dordrecht, The Netherlands: Kluwer Academic Publishers, 1994), pp. 1-38.

Applying the Gradient Magnitude algorithm

To run this algorithm, complete the following steps:

  1. Select Algorithms > Filter > Gradient Magnitude. The Gradient Magnitude dialog box opens (Figure 1).
  2. Complete the information in the dialog box.
  3. When complete, click OK. The algorithm begins to run.
A pop-up window appears with the status. The following message appears
"Calculating the Gradient Magnitude." When the algorithm finishes running, the pop-up window closes.
Depending on whether you selected New Image or Replace Image, the result appears in a new window or replaces the image to which the algorithm was applied.
Figure 1. Gradient Magnitude dialog box
X Dimension
Indicates the standard deviation (SD) of Gaussian in the X direction.
DialogboxGradientMagnitude.jpg
Y Dimension
Indicates the SD of Gaussian in the Y direction.
Z Dimension
Indicates the SD of Gaussian in the Z direction.
Use image resolutions to normalize Z scale
Normalizes the Gaussian to compensate for the difference if the voxel resolution is less between slices than the voxel resolution in-plane. This option is selected by default.
Process each slice independently (2.5D)
Blurs each slice of the dataset independently.
Process red channel
Applies algorithm to the red channel only.
Process green channel
Applies algorithm to the green channel only.
Process blue channel
Applies algorithm to the blue channel only.
New image
Shows the results of the algorithm in a new image window.
Replace image
Replaces the current active image with the results of the algorithm.
Whole image
Applies the algorithm to the whole image.
VOI region(s)
Applies the algorithm to the volumes (regions) delineated by the VOIs.
OK
Applies the Gradient Magnitude algorithm according to the specifications in this dialog box.
Cancel
Disregards any changes that you made in this dialog box and closes the dialog box.
Help
Displays online help for this dialog box.
Retrieved from "https://mipav.cit.nih.gov/pubwiki/index.php?title=Filters_(Spatial):_Gaussian_Blur&oldid=191"