Filters (Frequency) and Filters (Spatial): Adaptive Noise Reduction: Difference between pages
MIPAV>Olgavovk mNo edit summary |
MIPAV>Olgavovk mNo edit summary |
||
| Line 1: | Line 1: | ||
This algorithm reduces noise without blurring the edges by replacing a pixel value with a weighted sum of all local pixels reached by following a path with small pixel intensity values between neighboring pixels. | |||
=== Background === | === Background === | ||
The Adaptive Noise Reduction algorithm is a port to Adaptive Noise Removal Filter, a software program. This program first transforms ''RGB'' color space into ''YCrCb'' color space. When the filtering is complete, it then transforms the ''YCrCb'' color space into ''RGB'' color space. Hence, all of the color operations occur in ''YCrCb'' space. However, the program does not transform black-and-white images into another space. | |||
In "Frequently Asked Questions About Color," Charles Poynton reveals that the ''RGB''-to-''YCrCb'' and ''YCrCb''-to-''RGB'' conversion equations used in Adaptive Noise Removal Filter differ significantly from standard ones. First, the program creates an edge graph or pixel neighbor graph using a weakly median-filtered version of the ''YCrCb'' space. A weakly median-filter version means that median filtering only occurs if the pixel is not on an edge in ''Y'', ''Cr'', or ''Cb'' space. The edge graph is an array of arrays with the first array having a length equal to the number of pixels in the image and the second array having eight edge weights. The eight edge weights are calculated from the intensity differences between the center pixel and one of the eight neighboring pixels: | |||
<math> | |||
E =\sqrt{((dYwY)^2 + (dRwR)^2 + (dBwB)^2)} | |||
</math> | |||
**converting color;<br /> | |||
where ''E'' is the edge weight; ''dY'', ''dR'', and ''dB'' are the ''Y'', ''Cr'', and ''Cb'' differences; and ''wY'', ''wR'', and ''wB'' are the ''Y'', ''Cr'', and ''Cb'' weights derived from the ''Y'', ''Cr'', and ''Cb'' radiuses. A bigger relative radius results in a smaller weight for radiuses >= 0.1, which is typically the case. | |||
After the edge graph is created, the program filters the ''Y'', ''Cr,'' and ''Cb'' spaces separately. It uses the selected pixel as the center of a square with ''L'' = 2''R'' 1 where ''L'' = sides of length, ''R'' = range, and range = (int)(radius 0.999). | |||
The | The ''enhancePixel ''function returns the filtered pixel value at every pixel in the image. If neighboring pixels are connected to the center pixel via a low-cost path, queue elements corresponding to these neighboring pixels are added to the priority queue. If no queue element is retrieved from the queue, then the original pixel value is passed unchanged. If elements are retrieved from the queue, then those ''Y, Cr,'' or ''Cb'' pixel values that retrieved queue elements are put into a weighted sum. The weight is derived from an index into the filter array given by the queue element key times the invFilterLen. The filter array is generated with a Gaussian function. | ||
'' | Each queue element has a value, a baseKey, and a key. The ''value'' gives the location within the local [[Image:FiltersSpatialAdaptiveNoiseReduction8.jpg]] local square where ''R'' = range. The ''baseKey'' has a sum of the edgeGraph values over the low-cost path from the center pixel to the selected pixel, and ''key'' is equal to the sum of baseKey and the distMap value for the selected pixel. The distMap value at a given position inside the local square is equal to the edge preservation strength times the distance from the center pixel. A key is only added to the queue if key < maxDistance:'''' | ||
<math> | |||
M = (int)(Rd(S+512)) | |||
</math> | |||
'' | where ''M'' = maxDistance, ''Rd'' = radius, and ''S'' = edge preservation strength. | ||
The | The priority queue is implemented as a binary heap and the binary heap is implemented as an array. A binary heap is a nearly full binary tree (only the bottom level may not be complete). This binary heap has the property that for every node other than a leaf, its key value is less than or equal to that of its children. In a binary heap the item of highest priority is always at the root of the tree or at node 0. When the highest priority item at the root is removed, the item of highest priority among the remainder moves into the root position. The children of node ''i'' are at [[Image:FiltersSpatialAdaptiveNoiseReduction10.jpg]] and [[Image:FiltersSpatialAdaptiveNoiseReduction11.jpg]]. The parent of node ''i'' is at <math> | ||
(int) \left ( \frac {i-1}{2} \right ) | |||
</math>. | |||
The filter radius can be separately adjusted for each ''Y, Cr,'' and ''Cb'' channel for color images. For black-and-white images only, the ''Y'' filter radius can be adjusted. A larger radius removes more noise but loses more detail. | |||
and | |||
<div> | <div> | ||
{| border="1" cellpadding="5" | {| border="1" cellpadding="5" | ||
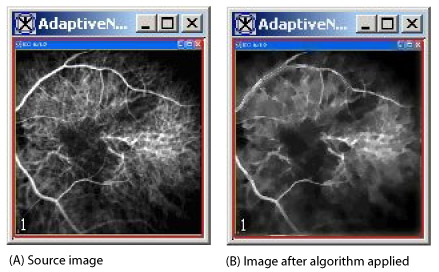
|+ <div>'''Figure 1. | |+ <div>'''Figure 1. Adaptive Noise Reduction processing''' </div> | ||
|- | |- | ||
| | | | ||
<div | <div><div><center>[[Image:exampleAdaptiveNoiseReduction.jpg]]</center></div> </div> | ||
|} | |} | ||
</div> | </div> | ||
The edge preservation strength can be adjusted. Larger values preserve more edges but sacrifice smoothness in low-contrast areas. Very large values may cause banding. | |||
To speed the filtering on color images, you can select the Filter ''Cr'' and ''C''b at halv''e''d dimensions check box. When run, the algorithm shrinks the Cr and'' Cb'' spaces by a factor of 2, generates an edge table for the shrunken space, filters the image, and then expands the filtered ''Cr'' and ''Cb'' spaces to their original dimensions. Although the algorithm runs faster, it also loses some details. | |||
The New image option causes MIPAV to place the resulting image in a new image window. The Replace image option causes MIPAV to place the changed image in the same window. | |||
==== Image types ==== | |||
You can apply this algorithm to both color and black-and-white 2D images. | |||
==== Special notes ==== | |||
None. | |||
==== References ==== | |||
=== | |||
Refer to the following references for more information: | |||
Karlis Freivalds, "Adaptive Noise Removal Filter," a software program, University of Latvia, Institute of Mathematics and Computer Science, at http://www.gradetools.com/karlisf. | |||
Charles Poynton, "Frequently Asked Questions About Color," at http://www.poynton.com. | |||
=== Applying the Adaptive Noise Reduction algorithm === | |||
To run this algorithm, complete the following steps: | To run this algorithm, complete the following steps: | ||
# Open an image | # Open an image. | ||
# Select Algorithms > Filters | # Perform, as an option, any image processing, such as improving the contrast, on the image. | ||
# Select Algorithms > Filters (spatial) > Adaptive noise reduction. The Adaptive Noise Reduction dialog box opens. | |||
# | # Complete the information in the dialog box. | ||
# | # Click OK. The algorithm begins to run. | ||
Depending on whether you selected | ; A pop-up window appears with the status. A series of status messages appear in the window. | ||
; When the algorithm finishes running, the pop-up window closes. | |||
; Depending on whether you selected New image or Replace image, the results appear in a new window or replace the image to which the algorithm was applied. | |||
<div> | <div> | ||
{| border="1" cellpadding="5" | {| border="1" cellpadding="5" | ||
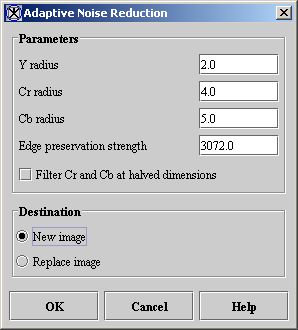
|+ <div>'''Figure | |+ <div>'''Figure 2. Adaptive Noise Reduction dialog box''' </div> | ||
|- | |- | ||
| | | | ||
<div>''' | <div>'''Y radius''' </div> | ||
| | | | ||
<div> | <div>Specifies the local square used for ''Y'' space filtering, which is approximately [[Image:FiltersSpatialAdaptiveNoiseReductionlz.jpg]]in size. </div><div>As the radius increases, the algorithm removes more noise, but loses more detail. The default value is 2.0. </div> | ||
| rowspan=" | | rowspan="2" colspan="1" | | ||
<div><div><center>[[Image: | <div><div><center>[[Image:dialogboxAdaptiveNoiseReduction.jpg]]</center></div> </div><div> </div> | ||
|- | |- | ||
| | | | ||
<div>''' | <div>'''Cr radius''' </div> | ||
| | | | ||
<div> | <div>Specifies the local square used for ''Cr ''space filtering (only available for color), which is approximately <div align="left">[[Image:FiltersSpatialAdaptiveNoiseReduction3.jpg]]</div> in size. </div><div>As the radius increases, the algorithm removes more noise, but loses more detail. The default value is 4.0. </div> | ||
|- | |- | ||
| | | | ||
<div> | <div>'''Cb radius''' </div> | ||
| | | rowspan="1" colspan="2" | | ||
<div> | <div>Specifies the local square used for ''Cb'' space filtering, which is approximately [[Image:FiltersSpatialAdaptiveNoiseReduction4.jpg]]in size. As the radius increases, the algorithm removes more noise but loses more detail. The default value is 5.0. </div> | ||
|- | |- | ||
| | | | ||
<div> | <div>'''Edge preservation strength''' </div> | ||
| rowspan="1" colspan="2" | | | rowspan="1" colspan="2" | | ||
<div> | <div>Specifies a value for preserving edges. Larger values preserve more edges but sacrifice smoothness in low-contrast areas. Very large values may cause banding. </div><div>For color images, the default value is 3072.0. For black-and-white images, the default value is [[Image:FiltersSpatialAdaptiveNoiseReduction5.jpg]] where ''IMx'' is image maximum and ''IMn'' is image minimum. </div> | ||
|- | |- | ||
| | | | ||
<div> | <div>'''Filter Cr and Cb at halved dimensions''' </div> | ||
| rowspan="1" colspan="2" | | | rowspan="1" colspan="2" | | ||
<div> | <div>Causes the algorithm to run faster but with some loss of detail. For color images, the default value is enabled; for other images, the default value is disabled. </div> | ||
|- | |- | ||
| | | | ||
<div>New image </div> | <div>'''New image''' </div> | ||
| rowspan="1" colspan="2" | | | rowspan="1" colspan="2" | | ||
<div> | <div>Shows the results of the algorithm in a new image window. </div> | ||
|- | |- | ||
| | | | ||
<div>Replace image </div> | <div>'''Replace image''' </div> | ||
| rowspan="1" colspan="2" | | | rowspan="1" colspan="2" | | ||
<div> | <div>Replaces the original source image with the results of the algorithm. </div> | ||
|- | |- | ||
| | | | ||
| Line 236: | Line 130: | ||
|- | |- | ||
| | | | ||
<div>'''Cancel''' </div> | <div>'''Cancel ''' </div> | ||
| rowspan="1" colspan="2" | | | rowspan="1" colspan="2" | | ||
<div>Disregards any changes | <div>Disregards any changes you made in this dialog box and closes the dialog box. </div> | ||
|- | |- | ||
| | | | ||
| Line 246: | Line 140: | ||
|} | |} | ||
</div> | |||
[[Category:Help]] | [[Category:Help]] | ||
[[Category:Help:Algorithms]] | [[Category:Help:Algorithms]] | ||
Revision as of 18:14, 18 May 2012
This algorithm reduces noise without blurring the edges by replacing a pixel value with a weighted sum of all local pixels reached by following a path with small pixel intensity values between neighboring pixels.
Background
The Adaptive Noise Reduction algorithm is a port to Adaptive Noise Removal Filter, a software program. This program first transforms RGB color space into YCrCb color space. When the filtering is complete, it then transforms the YCrCb color space into RGB color space. Hence, all of the color operations occur in YCrCb space. However, the program does not transform black-and-white images into another space.
In "Frequently Asked Questions About Color," Charles Poynton reveals that the RGB-to-YCrCb and YCrCb-to-RGB conversion equations used in Adaptive Noise Removal Filter differ significantly from standard ones. First, the program creates an edge graph or pixel neighbor graph using a weakly median-filtered version of the YCrCb space. A weakly median-filter version means that median filtering only occurs if the pixel is not on an edge in Y, Cr, or Cb space. The edge graph is an array of arrays with the first array having a length equal to the number of pixels in the image and the second array having eight edge weights. The eight edge weights are calculated from the intensity differences between the center pixel and one of the eight neighboring pixels:
- converting color;
- converting color;
where E is the edge weight; dY, dR, and dB are the Y, Cr, and Cb differences; and wY, wR, and wB are the Y, Cr, and Cb weights derived from the Y, Cr, and Cb radiuses. A bigger relative radius results in a smaller weight for radiuses >= 0.1, which is typically the case.
After the edge graph is created, the program filters the Y, Cr, and Cb spaces separately. It uses the selected pixel as the center of a square with L = 2R 1 where L = sides of length, R = range, and range = (int)(radius 0.999).
The enhancePixel function returns the filtered pixel value at every pixel in the image. If neighboring pixels are connected to the center pixel via a low-cost path, queue elements corresponding to these neighboring pixels are added to the priority queue. If no queue element is retrieved from the queue, then the original pixel value is passed unchanged. If elements are retrieved from the queue, then those Y, Cr, or Cb pixel values that retrieved queue elements are put into a weighted sum. The weight is derived from an index into the filter array given by the queue element key times the invFilterLen. The filter array is generated with a Gaussian function.
Each queue element has a value, a baseKey, and a key. The value gives the location within the local ![]() local square where R = range. The baseKey has a sum of the edgeGraph values over the low-cost path from the center pixel to the selected pixel, and key is equal to the sum of baseKey and the distMap value for the selected pixel. The distMap value at a given position inside the local square is equal to the edge preservation strength times the distance from the center pixel. A key is only added to the queue if key < maxDistance:'
local square where R = range. The baseKey has a sum of the edgeGraph values over the low-cost path from the center pixel to the selected pixel, and key is equal to the sum of baseKey and the distMap value for the selected pixel. The distMap value at a given position inside the local square is equal to the edge preservation strength times the distance from the center pixel. A key is only added to the queue if key < maxDistance:'
where M = maxDistance, Rd = radius, and S = edge preservation strength.
The priority queue is implemented as a binary heap and the binary heap is implemented as an array. A binary heap is a nearly full binary tree (only the bottom level may not be complete). This binary heap has the property that for every node other than a leaf, its key value is less than or equal to that of its children. In a binary heap the item of highest priority is always at the root of the tree or at node 0. When the highest priority item at the root is removed, the item of highest priority among the remainder moves into the root position. The children of node i are at ![]() and
and ![]() . The parent of node i is at .
. The parent of node i is at .
The filter radius can be separately adjusted for each Y, Cr, and Cb channel for color images. For black-and-white images only, the Y filter radius can be adjusted. A larger radius removes more noise but loses more detail.
The edge preservation strength can be adjusted. Larger values preserve more edges but sacrifice smoothness in low-contrast areas. Very large values may cause banding.
To speed the filtering on color images, you can select the Filter Cr and Cb at halved dimensions check box. When run, the algorithm shrinks the Cr and Cb spaces by a factor of 2, generates an edge table for the shrunken space, filters the image, and then expands the filtered Cr and Cb spaces to their original dimensions. Although the algorithm runs faster, it also loses some details.
The New image option causes MIPAV to place the resulting image in a new image window. The Replace image option causes MIPAV to place the changed image in the same window.
Image types
You can apply this algorithm to both color and black-and-white 2D images.
Special notes
None.
References
Refer to the following references for more information:
Karlis Freivalds, "Adaptive Noise Removal Filter," a software program, University of Latvia, Institute of Mathematics and Computer Science, at http://www.gradetools.com/karlisf.
Charles Poynton, "Frequently Asked Questions About Color," at http://www.poynton.com.
Applying the Adaptive Noise Reduction algorithm
To run this algorithm, complete the following steps:
- Open an image.
- Perform, as an option, any image processing, such as improving the contrast, on the image.
- Select Algorithms > Filters (spatial) > Adaptive noise reduction. The Adaptive Noise Reduction dialog box opens.
- Complete the information in the dialog box.
- Click OK. The algorithm begins to run.
- A pop-up window appears with the status. A series of status messages appear in the window.
- When the algorithm finishes running, the pop-up window closes.
- Depending on whether you selected New image or Replace image, the results appear in a new window or replace the image to which the algorithm was applied.
|
Y radius
|
As the radius increases, the algorithm removes more noise, but loses more detail. The default value is 2.0.
|
|
|
Cr radius
|
Specifies the local square used for Cr space filtering (only available for color), which is approximately in size. As the radius increases, the algorithm removes more noise, but loses more detail. The default value is 4.0.
| |
|
Cb radius
|
||
|
Edge preservation strength
|
Specifies a value for preserving edges. Larger values preserve more edges but sacrifice smoothness in low-contrast areas. Very large values may cause banding.
| |
|
Filter Cr and Cb at halved dimensions
|
Causes the algorithm to run faster but with some loss of detail. For color images, the default value is enabled; for other images, the default value is disabled.
| |
|
New image
|
Shows the results of the algorithm in a new image window.
| |
|
Replace image
|
Replaces the original source image with the results of the algorithm.
| |
|
OK
|
Applies the algorithm according to the specifications in this dialog box.
| |
|
Cancel
|
Disregards any changes you made in this dialog box and closes the dialog box.
| |
|
Help
|
Displays online help for this dialog box.
| |