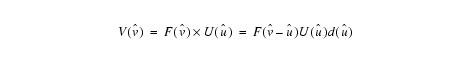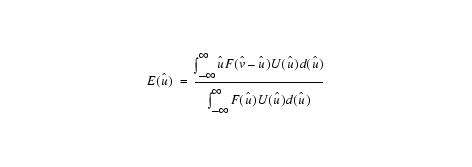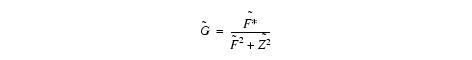Shading Correction: Inhomogeneity N3 Correction
This preprocessing algorithm corrects for shading artifacts often seen in MRI. The heart of the algorithm is an iterative approach that estimates both a multiplicative bias field and a distribution of true tissue intensities. Referred to as nonparametric intensity nonuniformity normalization (N3), this method makes no assumptions about the kind of anatomy present in a scan and is robust, accurate, and fully automatic.
Contents
Background
A common difficulty with tissue intensity model based methods is the determination of the model. The modeling assumption in the N3 algorithm is that nonuniformity blurs the histogram of the data in a way that it can be identified, quantified, and removed. This nonuniformity blurring distribution is referred to as the blurring kernel F. The following equation is the basis of the N3 method:
Equation 1Where at location x, v is the measured signal, u is the true signal emitted by the tissue, f is an unknown smoothly varying bias field, and n is white Gaussian noise assumed to be independent of u. As can be seen, the unknown smoothly varying bias field f multiplies the true signal u, thereby corrupting it. Then the additive noise n is added, resulting in the output measured signal v. To compensate for the intensity nonuniformity, the first task is to estimate its distribution, or f.
Then taking the log of all parameters, we are left with ^u = log(u) and ^f=log(f), both of which we assume to be independent or uncorrected random variables of probability densities U, V, and F. Then substituting these variables back into equation 1 and converting the equation of distributions into one of probability densities, the distribution of their sum turns into the following convolution, see equation 2
Equation 2Equation 2 models the nonuniformity distribution F viewed as blurring the intensity distribution U.
Now the model of intensity nonuniformity used here is that of a multiplicative field corrupting the measured intensities. However, viewing the model from a signal processing perspective, one sees that there is a much more specific consequence, a reduction of only high-frequency components of U. Thus, the approach used in the N3 algorithm to correct for nonuniformity turns into an optimization problem, which goal is to maximize the frequency contents of U.
How the N3 method works
We begin with only a measured distorted signal, or image, which we call v. For computational purposes, we do not deal with simple v, but instead, with log^v and the histogram distribution of the log, and use ^v to denote V. The same representations are used for the true signal, u, and the distortion signal, f.
The model assumed here is that of a multiplicative biasing field that multiplies the true signal to distort it, thereby creating a signal with induced field inhomogeneity. So, just as a multiplication takes place to corrupt the field, a division should undo the corruption. Now carrying this idea over to the frequency domain where all of the computations take place, multiplications turn into convolutions and divisions turn into deconvolutions.
To begin with, all one has is v. Users provide a value for the kernel full-width, half maximum (FWHM) of f. Then, the iteration takes place as this estimate of f is later used to compute U and then U input back into the algorithm to create another mapping, another f, and hence another U. The process then repeats until convergence. The result is an estimated true value of U.
Mapping from v to f
The approach adopted for finding U depends largely on the mapping from v to f. The idea is to propose a distribution of U by sharpening the distribution V and then estimating the corresponding smooth field log(f), which produces a distribution U close to the one proposed. However, rather than searching through the space of all distributions U, one can take advantage of the simple form of the distribution F. Suppose the distributions of F is Gaussian. Then one need only search the space of all distributions U corresponding to Gaussian distributed F having zero mean and given variance. In this way the space of all distributions U is collapsed into a single dimension, the width of the F distribution. Thus, concludes the mapping N3 creates from v to f.
Estimating u throughout an entire volume:
Equation 3
Estimating u (voxel by voxel):
Equation 4
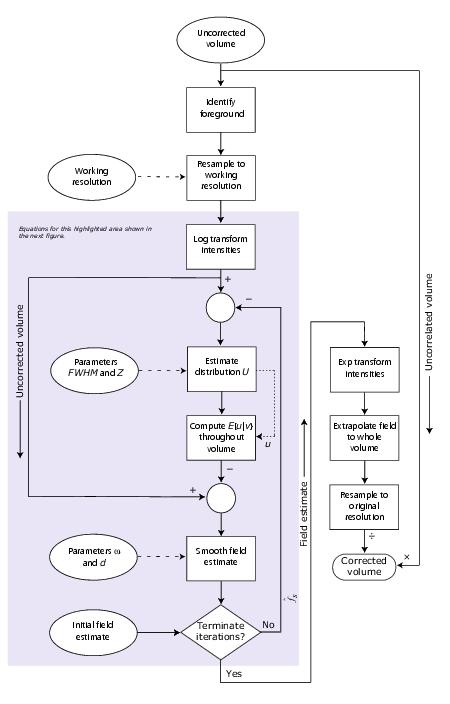
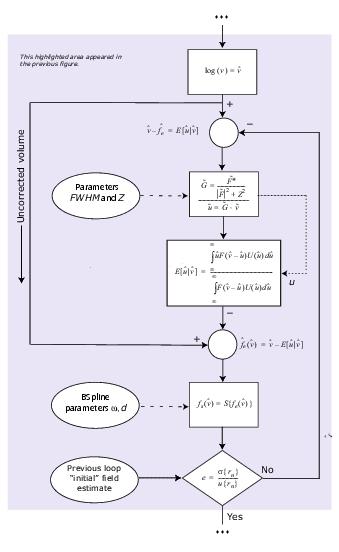
Algorithm flow chart
This algorithm performs the process shown in the flow chart in Figure 1. What was previously described was just the basic algorithm idea. The equations behind the steps in the process are shown in an enlarged section of the flow chart in Figure 2.
The algorithm does the following:
- Identifies the foreground. In this step, the algorithm thresholds the background.
- Resamples to working resolution. Use the input working resolution "subsampling factor."
- Logs transform intensities.
- Obtains the expectation of the real signal. Given a measured signal, the algorithm obtains the expectation of the real signal by performing a voxel by voxel difference between the logs of signal and estimate bias field.
- Obtains an initial estimate of distribution U. The algorithm estimates distribution U, where U is a sharpened distribution of V. The sharpening is done using input parameters FWHM and Z. Given a distribution F and the measured distribution of intensities V, the distribution U can be estimated using a deconvolution filter as follows:
Equation 5
Equation 6
where
F* denotes complex conjugate
'~F is the fourier transform of F
Z is a constant term to limit the magnitude of ~G
This estimation of U is then used to estimate the corresponding field.
- Computes the expectation of real signal-The algorithm computes the expectation of the real signal given measured signal (both logged). Full volume computation done using distributions U and Gaussian blurring kernel F (whose FWHM parameter is given by users). A basic mapping from v to f. This is the iterative portion, which is shown the main loop in Figure 1.
- Obtains a new field estimate-The difference between the measured signal and the newly computed expectation of the real signal given the measured signal (all variables logged).
Equation 7
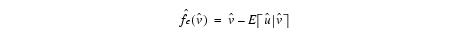
- Smooths the bias field estimate-Using the B-spline technique with the parameter d field distance input provided by users.
Equation 8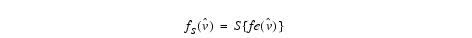
- Terminates iterations-The algorithm then checks for the convergence of field estimates. If the subsequent field estimate ratio becomes smaller than the end tolerance parameter input by users, the iterations are terminated. If not, a new F is used in step 2, and the iteration repeats step 4 through step 9.
Equation 9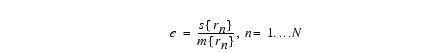
where r'n is the ratio between subsequent field estimates at the n-th location, s -denotes standard deviation, and m denotes mean. Typically after 10 iterations, e drops below 0.001.- Completes the final steps-Given the measured signal, obtain the expectation of the real signal by calculating a voxel by voxel difference between logs of signal and an estimate of the bias field. Once iteration is complete, exponential transform intensities V and F, extrapolate field to volume, resample data back to original solution. Then divide v by f. The result is u.
Equation 10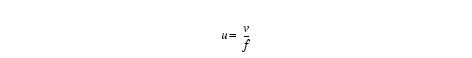
Figure 1. Flow chart describing the N3 method
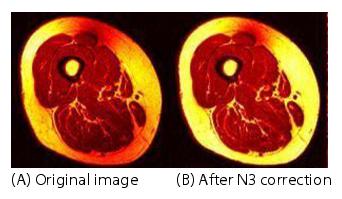
Figure 3. The effect of N3 on an image: (A) original image and (B) image after N3 correction
Figure 3 shows an original image A and the image B produced from using the best N3 paratmeters:
- Treshold = 100
- Maximum iterations = 100
- End tolerance = 0.0001
- Field distance = 33.33
- Subsampling factor = 2
- Kernel FWHM = 0.8
- Wiener = 0.01
Figure 4 shows an original image and the effect of different parameters used in the Inhomogeneity N3 Correction algorithm on the image.
Figure 4. The effects of different settings for the Inhomogeneity N3 algorithm on an image 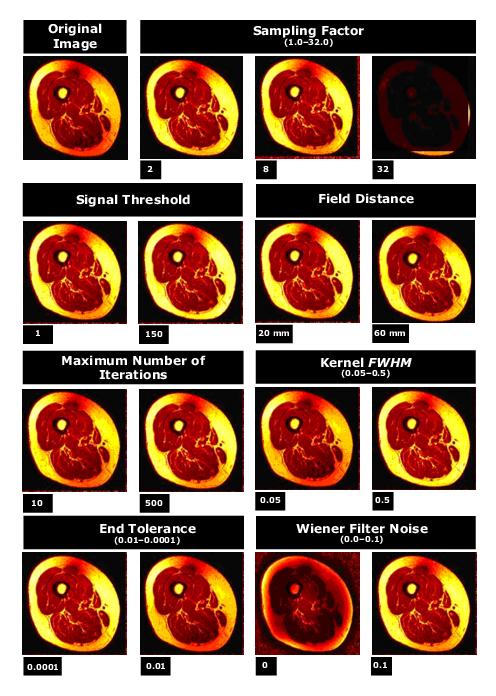
Image Types
One can apply this algorithm only to 2D and 3D MRI images.
Applying the Inhomogeneity N3 algorithm
To run this algorithm, complete the following steps:
- Open an image.
- Select Algorithms > Shading correction > Inhomogeneity N3 correction. The N3 Inhomogeneity Correction dialog box opens.
- Complete the information in the dialog box (refer to "Choosing good parameters for N3 Algorithm" for advice on which values to select.
- Click OK. The algorithm begins to run.
- A pop-up window appears with the status. A series of status messages appear in the window.
- When the algorithm finishes running, the pop-up window closes.
- Depending on whether you selected New image or Replace image, the results appear in a new window or replace the image to which the algorithm was applied.
Choosing good parameters for N3 Algorithm
Signal threshold-Check the histogram for the minimum image values in the image. Make sure these values are smaller than the shading artifact. Generally, this value is about 100. To save time, use as high a threshold as possible.
Maximum number of iterations-Generally, this parameter is only important if you wish to terminate the process early by entering a number short of the number of iterations necessary for the algorithm to complete the process. However, to allow the algorithm to work to completion, a safe value to enter would be at least 100. Making it too high should have no consequence.
End tolerance-When the remaining parameters are chosen optimally, this parameter tends not to have much of an affect. However, with less effective parameters, the end tolerance can make a large difference, bringing the algorithm to work at least sparsely on large artifacts when a minimal end tolerance is chosen. The alternative is a high end tolerance, which can bring the shading correction to be almost nonexistent. In this case, the default value for this parameter is generally all right. For best results, however, use 0.0001. As far as timing, even with the minimum value, the processing time does not vary much.
Field distance-A large field distance takes all shading artifacts to be large. Small independent ones are ignored, while small clustered ones are smeared into one. So with large smear-like gradual (light) artifacts, a large parameter works well. However, a small field distance is much more precise. Every little artifact is independently corrected, and the intensity with which the algorithm works is much higher as can be noted in the field images. The field image of an image corrected with a small field distance has several dark clusters, generally distributed throughout the image even to parts where artifact may not be noticeable even to users. The field image of an image corrected with a large field distance may have one or two large smears, and nothing more.
The main trade-off here is time. Very small field distances can increase the processing time immensely. So the lowest one should go for optimal results yet without spending too much time on one image, which has been found to be about 10. That value should really only be used with several intense and isolated artifacts. For regular images a third of the default is sufficient. For quick results or for artifacts largely spread and not too strong, choose a value that is a little less than the default value, but more than half of the default value.
Subsampling-For best results, specify 1. However, keep in mind that the higher the precision (lower the subsampling), the higher the likelihood that certain low-intensity pixels inside the image are treated as background creating a speckle artifact.
Kernel FWHM-Use 0.5.
Wiener-Use 0.01.
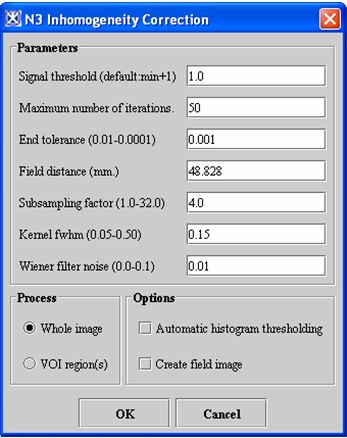
N3 Inhomogeneity Correction dialog box
Signal threshold
Treats those voxels of intensity that are lower than this threshold value as background. The default value is 1.0.
Max number iterations
Specifies the maximum number of iterations allowed before the process is terminated. The default value is 50.
End tolerance
Specifies convergence when all membership functions (of the fuzzy C cluster segmentation) over all pixel locations j change by less than this tolerance value between two iterations. The default value is 0.001.
Field distance
Specifies the characteristic distance over which the field varies. The distance between adjacent knots in B-spline fitting with at least 4 knots going in every dimension. The automatic default is one third of the distance (resolution * extents) of the smallest dimension.
Subsampling Factor
Specifies the value by which data is subsampled to a lower resolution in estimating the slowly varying nonuniformity field. It reduces sampling in the finest sampling direction by the shrink factor. Sampling in other directions is reduced only if reduced sampling in direction of finest resolution is less than current sampling. The default value is 4.
Kernel FWHM
Specifies the width of deconvolution kernel F (a Gaussian) used to sharpen the V(pdf of log(v), where v is the measured signal) histogram. Larger values give faster convergence while smaller values give greater accuracy. The default value is 0.01.
Wiener Filter Noise
Whole image
Applies the algorithm to the whole image.
VOI region(s)
Applies the algorithm to the volumes (regions) delineated by the VOIs.
Automatic histogram thresholding
Computes a threshold value through histogram analysis that should remove just the background from the computation. Selecting this check box disables the Signal threshold box, the Whole image, and VOI regions.
Create field image
Indicates whether to create a field image.
OK
Applies the algorithm according to the specifications in this dialog box.
Cancel
Disregards any changes you made in this dialog box and closes the dialog box.
Help
Displays online help for this dialog box.
References
Refer to the following sources for more information about the N3 algorithm.
Sled, John G., Alex P. Zijdenbos, and Alan C. Evans. "A Nonparametric Method for Automatic Correction of Intensity Nonuniformity in MRI Data." IEEE Transactions on Medical Imaging, 17(February 1998):87-97.
Sled, John G. "A Non-Parametric Method for Automatic Correction of Intensity Non-uniformity in MRI Data." Masters thesis, Department of Biomedical Engineering, McGill University, May 1997. - Smooths the bias field estimate-Using the B-spline technique with the parameter d field distance input provided by users.