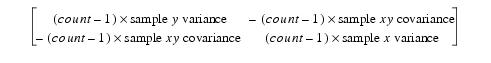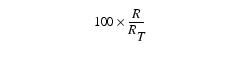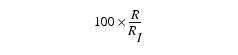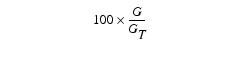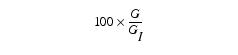Microscopy Colocalization Orthogonal Regression
This algorithm quantifies automatically the amount of colocalization in images. Recently, this method was used to quantify protein-protein interactions from colocalization data analysis of two-color confocal microscope images. The method was accurate enough to determine dissociation rates of two interacting proteins labeled with fluorescence reporters in live cells. This method may be helpful in answering other biological questions that involve protein-protein interactions or co-compartmentalization.
| Disclaimer: Colocalization cannot distinguish interaction from co-compartmentalization for compartments below light resolution (i.e., distances less than 200 nm). |
The theory of colocalization assumes that a high level of similarity between two spatial patterns implies proximity of the two proteins, which implies direct or indirect protein binding, or co-compartmentalization, of the proteins.
Specifically, the algorithm creates a 2D histogram from two colors of a single image or from two black-and-white images. It uses an orthogonal line fit of the histogram data to generate a correlation line through the histogram. Upper right region rectangles with lower left corners on the correlation line are used as colocalization regions, regions where both of the two colors are significantly above background. The colocalization frame is tied to the original or modified source image or images, therefore only the pixels located in the colocalization region are displayed. A user-movable point allows for the display of source image pixels and statistics associated with different upper right colocalization regions. When not in free range mode, the point must move along the correlation line. In free range mode, the point can move anywhere in the histogram buffer.
In summary regarding the usage of this algorithm, one must make sure that the images acquired have low noise levels and no bleed through and that the optical setup used for each color leads to the same point spread function (PSF) and is free of registration errors. Assumptions made in this approach are that pixel intensities linearly relate to concentration of molecular species being measured and that a pixel is either colocalized or not.
Contents
Background
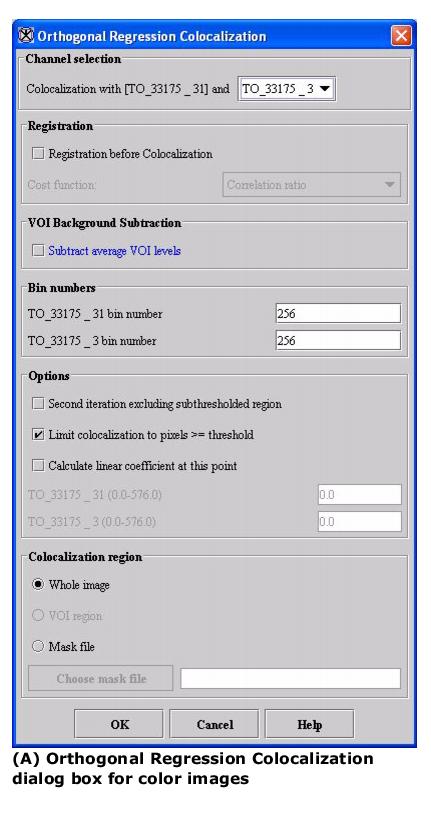
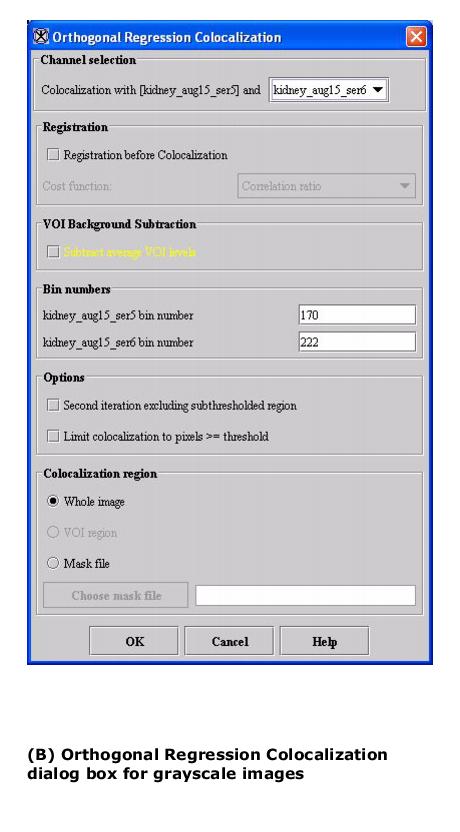
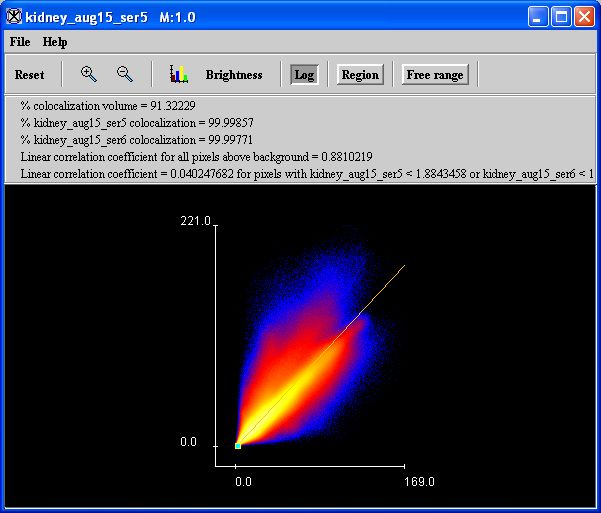
Based on the type of image, when this algorithm is used, either the Orthogonal Regression Colocalization dialog box for color images or the Orthogonal Regression Colocalization dialog box for grayscale images (see Figure 1) opens.
As an option, the Colocalization Orthogonal Regression algorithm can perform background level subtraction on images. If the Subtract average VOI level check box is selected, then the algorithm calculates the average pixel levels in the yellow VOI in one-color images or in the two yellow VOIs in two black-and-white images. It then subtracts these two background levels from the 1 or 2 source images. If a registration was also selected, the background determinations occur before registration, and subtraction occurs after the registration. After the subtraction is performed, any pixels with negative values are set to zero.
As an option this algorithm can perform image registration before performing colocalization. If you select the Registration before Colocalization check box on the Orthogonal Regression Colocalization dialog box, this algorithm runs another algorithm-the Optimized Automatic Registration (OAR) 2D algorithm-first. In this registration, both images or colors are moved halfway to a common center point. The registration is always done on the entire image. The only registration parameter that you can vary is the cost function. Although correlation ratio is the default cost function, you can select least squares, normalized cross correlation, or normalized mutual information instead.
After registration, this algorithm performs colocalization on the registered image or images rather than on the original image. After subtraction, this algorithm performs colocalization on the subtracted image or images rather than on the original image. If the maximum data range is decreased, then the number of histogram bins decreases if necessary so as not to exceed the actual number of channels in the data range.
The amount of colocalization can be measured with the linear correlation coefficient.
- Let L be the linear correlation coefficient
- Let the two channels be R and G
- Let the average values be
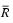 and
and 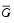
Then
<math> L = \frac {\sum_i ((R_i - \bar {R}) (G_i - \bar{G}))} {\sqrt {\sum ((R_i - \bar {R})^2) \sum ((G_i - \bar {G})^2)}} </math>
This is equivalent to the more traditional form of the equation:
<math> \frac {\left ( N\sum R_iG_i \right ) - \left ( \sum R_i \sum G_i \right )} {\left ( \sqrt {N \sum R^2_i - \left ( \sum R_i \right )^2 }\right )\left ( \sqrt {\left ( N \sum G^2_i \right ) - \left ( \sum G_i \right )^2} \right )} </math>
where N is the number of pixels.
The linear correlation coefficient ranges from -1 to 1 with 0 the value for random patterns and 1 the value for 100-percent colocalization. Negative values of the coefficient are not used for colocalization since that would indicate an anticolocalized situation with a bright pixel in one channel implying a dim pixel in another channel.
| Note: The medical literature on colocalization refers to the traditional linear correlation coefficient as Pearson's coefficient. |
This algorithm uses the linear least squares method of calculating the best line fit for ![]() . It uses an orthogonal line fit where the minimized distance measurements are orthogonal to the proposed line. This is an orthogonal regression as opposed to a traditional direct regression of dependent y variable green on independent red variable x, which would minimize the vertical distances between the points and the fitted line. An inverse regression of red on green would minimize the horizontal distances between the points and the fitted line. All three lines pass through the point (
. It uses an orthogonal line fit where the minimized distance measurements are orthogonal to the proposed line. This is an orthogonal regression as opposed to a traditional direct regression of dependent y variable green on independent red variable x, which would minimize the vertical distances between the points and the fitted line. An inverse regression of red on green would minimize the horizontal distances between the points and the fitted line. All three lines pass through the point (![]() ,
, ![]() ), but the three lines only coincide if the correlation coefficient equals -1 or 1. Use of a direct regression only makes sense if one variable is dependent and one variable is independent. Since the red and green dyes used in colocalization are best thought of as two independent variables, the orthogonal regression is most appropriate.
), but the three lines only coincide if the correlation coefficient equals -1 or 1. Use of a direct regression only makes sense if one variable is dependent and one variable is independent. Since the red and green dyes used in colocalization are best thought of as two independent variables, the orthogonal regression is most appropriate.
| Note: Orthogonal regression is also called total least squares. |
Points that are part of the dataless background in both images are excluded from the regression line calculations. Let R be the red channel and G be the green channel. If ![]() and
and ![]() , the point i is not included in the regression line calculations. If the image is not a floating point image, background1= 1.0 and background2 =1.0. In floating point images, the image minimums are used as backgrounds so that no points are excluded. Note that there are two VOIs: the yellow background subtraction VOI and a nonyellow VOI used to delineate the region of the image included in calculations. You can select to use points from the entire image, only points from the contour VOI region, or only points allowed by a mask file.
, the point i is not included in the regression line calculations. If the image is not a floating point image, background1= 1.0 and background2 =1.0. In floating point images, the image minimums are used as backgrounds so that no points are excluded. Note that there are two VOIs: the yellow background subtraction VOI and a nonyellow VOI used to delineate the region of the image included in calculations. You can select to use points from the entire image, only points from the contour VOI region, or only points allowed by a mask file.
| Tip: If VOI region is selected, then, after the algorithm is run, you can move the VOI by dragging it with the mouse to another region on the image. When the mouse button is released, the calculation is performed again updating the histogram. This allows the calculation to be performed with the same contour VOI in different positions. |
The optional second iteration, thresholding, is different from the first iteration thresholding. In the first iteration, points are only excluded if they are below both background1 and background2. However, in the second iteration, points are excluded if they are below either lastPositive1 or lastPositive2. The (lastPositive1, lastPositive2) is the last point going from top to bottom on the first iteration regression line before an L-shaped subthreshold region with a zero or negative linear correlation coefficient is found. In the second iteration, the L-shaped subthreshold region determined from the first iteration is excluded from the regression line calculations. The default is to not perform a second iteration.
The slope and offset of the orthogonal regression line can be obtained from the eigenvector of the smallest eigenvalue of the 2 by 2 matrix:
The eigenvector has the components (direction x, direction y).
<math> slope of the line = \frac {direction y} {direction x} = \frac {V_y -V_x + \sqrt {(V_y -V_x)^2 (4Cxy^2)}} {2Cxy} </math>
where
- S = slope of the line
- V= variance
- C = covariance
<math> offset = \bar{y} - S (\bar {x}) </math>
- Let n be the normal vector to the orthogonal regression line.
- Let theta be the angle from the x axis to the normal.
<math> n = \bar{x} cos \theta + \bar {y} sin \theta </math>
where
<math> \theta = arctan (slope) </math>
The minimized residue, the mean square error (MSE), is given by the following: <math> MSE = variance x (cos \theta)^2 + covariance xy (sin 2 \theta) +variance y (sin \theta)^2 = \frac {variance x + 2slope (covariance xy) + slope ^2 (variance y)} {1+ slope ^2} </math>
A histogram buffer is generated with bin1 counts along the x axis and bin2 counts along the y axis. The Orthogonal Regression Colocalization dialog box allows you to specify the two bin numbers. The default is the range of the data (max - min 1) or 256, whichever is less, for nonfloating point images and 256 for floating point images.
The algorithm calculates the linear correlation coefficients for all pixels whose values are either below threshold in buffer or are below ![]() in secondBuffer. This is the L-shaped subthreshold region. The algorithm calculates along the color that has the greatest range along the line segment. The line segment's (color1,color2) point just above the point where the linear correlation coefficient becomes negative or zero is taken in a nonrigorous fashion as the threshold point separating upper right rectangular colocalized data from the lower left L-shaped noncolocalized data.
in secondBuffer. This is the L-shaped subthreshold region. The algorithm calculates along the color that has the greatest range along the line segment. The line segment's (color1,color2) point just above the point where the linear correlation coefficient becomes negative or zero is taken in a nonrigorous fashion as the threshold point separating upper right rectangular colocalized data from the lower left L-shaped noncolocalized data.
The algorithm calculates the percent colocalization area, the percent red colocalization, and the percent green colocalization. Each point has a red value = threshold and a green value = secondThreshold. Thus, each point defines an upper right rectangular region characterized by ![]() and
and ![]() .
.
The percent colocalization area is 100 times the number of pixels belonging to the upper right rectangular region divided by the number of pixels in the entire image or selected VOI.
|
Percent
|
If Limit colocalization to pixels >= threshold is . . .
| |
|---|---|---|
|
Selected
|
Not selected (default)
| |
|
Red colocalization
|
where R = Sum of the red values in the upper right rectangular region
|
where R = Sum of the red values in the upper right rectangular region
|
|
Green colocalization
|
where G = Sum of the green values in the upper right rectangular region
|
where G = Sum of the green values in the upper right rectangular region
|
| Note:Only pixels with at least one of the two levels above background that you specify in the Orthogonal Regression Colocalization dialog box are included in any of the above sums. |
Images types
You can apply this algorithm to both color and black-and-white 2D or 3D images.
Special notes
Limitations to colocalization include the following:
- The inability to distinguish binding proteins from nonbinding proteins located within a cellular compartment smaller than the resolution of light microscopes (rough 200 nm)
- All current colocalization methods, including this one, force each pixel to be classified as either entirely colocalized or entirely noncolocalized signals. Clearly, this is not the case. Unfortunately, a method that treats each pixel as the sum of colocalized and noncolocalized signals has not been developed yet.
- An important note regarding quantitative colocalization is the need to use low-noise images to make accurate measurements since two identical signals become more and more uncorrelated as their signal-to-noise ratio decreases. The amount of noise in a region of interest can be determined by measuring the Pearson correlation coefficient of two consecutive acquisitions of the same channel. For example, one could try to keep all images with a correlation above 90 percent (e.g., increasing laser power, using more averages). Also, in order to compute accurately each colocalized fraction, the background must be subtracted from each channel.
- Other important notes regarding the usage of this algorithm: One must make sure that the images acquired have low-noise levels and no bleedthrough, and the optical setup used for each color leads to the same PSF and is free of registration errors. Assumptions made in this approach are that pixel intensities linearly relate to concentration of molecular species being measured and that a pixel is either colocalized or not.
References
See the following references for more information about this algorithm:
Sylvain V. Costes, Dirk Daelemans, Edward H. Cho, George Pavlakis, and Stephen Lockett, "Protein-protein interaction quantified by microscopic co-localization in live cells."
Gishan Dissanaike and Shiyun Wang, Equations for slope and offset of the orthogonal least squares problem, "A Critical Examination of Orthogonal Regression and an application to tests of firm size interchangeability."
E. M. M. Manders, J. Stap, G. J. Brakenhoff, R.Van Driel, and J. A. Aten, "Dynamics of three-dimensional replication patterns during the S-phase, analysed by double labelling of DNA and confocal microscopy," Journal of Cell Science, 103:857-862, 1992.
E. M. M. Manders, F. J. Verbeek, and J. A. Aten, "Measurement of co-localization of objects in dual-colour confocal images," Journal of Microscopy, Vol. 169, Pt. 3:375-382, March 1993.
Eigenvalue software for solving the orthogonal least squares problem is found at the internet site www.magic-software.com.
Jan A. Van Mieghem, Hadar I. Avi-Itzhak, and Roger D. Melen, Equations for slope and mean square error of the orthogonal least squares from "Straight Line Extraction Using Iterative Total Least Squares Methods," Journal of Visual Communication and Image Representation, Vol. 6, No. 1, pp. 59-68, March 1995.
Applying the algorithm
To run this algorithm, complete the following steps:
- Open either one color or two black-and-white images.
- Select Algorithms > Microscopy > Colocalization > Orthogonal Regression.
- Depending on whether the image is grayscale or color, the Orthogonal Regression dialog box for grayscale images (Figure 1) or the Orthogonal Regression box for color images (Figure 2) opens.
- Complete the information in the dialog box.
- Click OK.
- The algorithm begins to run, and a progress bar appears with the status. When the algorithm finishes running, the progress bar disappears, and a 2D histogram with a correlation line and statistics for the threshold point appears in a new window.
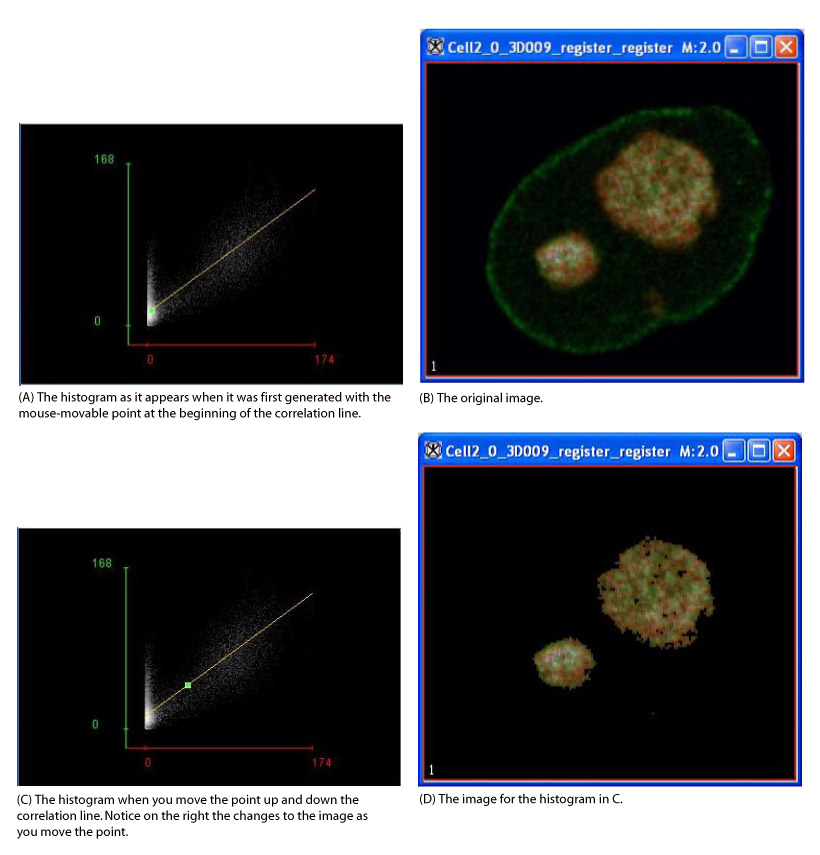
- Use the mouse to move the point to see the statistics for different upper right rectangular colocalization regions. This colocalization frame is tied to the original or modified color source image or to the two original or modified grayscale source images. Only those pixels belonging to the upper right colocalization regions are visible in the source images. If you want to move the point off the line, select Free range mode.
- If you created a VOI on the source image and selected the VOI region in the dialog box, then you can drag the VOI with the mouse. When you release the mouse, the algorithm recalculates using the new VOI position and updates the histogram.
|
|
| |
|
Channel selection
|
Color images: Specifies the colors to use in color images.
Grayscale images: Specifies the second grayscale image to be used. Select one from the list box.
| |
|
Registration before colocalization
|
Performs registration on an entire image before performing colocalization. When you select Registration before colocalization, the Cost function box becomes available. By default, registration is not selected.
| |
|
Cost function
|
Specifies the cost function to be used during registration. You can specify correlation ratio (default), least squares, normalized cross correlation, or normalized mutual information. To make this box available, you must first select Registration before colocalization.
| |
|
VOI background subtraction
|
Calculates the average background levels in the yellow VOI and subtracts them from the rest of the image if Subtract average VOI level is selected. The subtraction results are clamped to be >= zero. The default is no subtraction.
| |
|
Bin numbers
|
Specifies the number of histogram bins to be used in the 2D histogram. The default is the range of the data or 256, whichever is less, for nonfloating point images and 256 for floating point images.
| |
|
Options
|
Second iteration excluding subthresholded region-Excludes the L-shape subthreshold region determined from the first iteration from the regression line calculations. By default, this check box is clear.
| |
|
Limit colocalization to pixels >= threshold-Uses, in red colocalization, only pixels with red values >= red threshold in the denominator sum and, in green colocalization, only pixels with green values >= green threshold in the denominator sum. The default value is not selected.
| ||
|
Colocalization region
|
Whole image-Makes calculations on the whole image. By default, this option is selected.
| |
|
VOI region-Makes calculations on only the pixels in the VOI. To enable this option, a contour VOI must be present in the image. After this algorithm run and the histogram is produced, if you drag the VOI with the mouse and then release the mouse button, the system recalculates using the new VOI position.
| ||
|
Mask file-Makes calculations on only the pixels in the mask. Selecting this option enables the Choose mask file button.
| ||
|
Choose mask file-Allows you to select a mask file.
| ||
|
Free range
|
Toggles between requiring the point to be in the least squares line and allowing the point to be anywhere in the histogram buffer. By default, the free range mode is not selected.
| |
|
OK
|
Applies the algorithm according to the specifications in this dialog box.
| |
|
Cancel
|
Disregards any changes that you made in this dialog box and closes the dialog box.
| |
|
Help
|
Displays online help for this dialog box.
| |
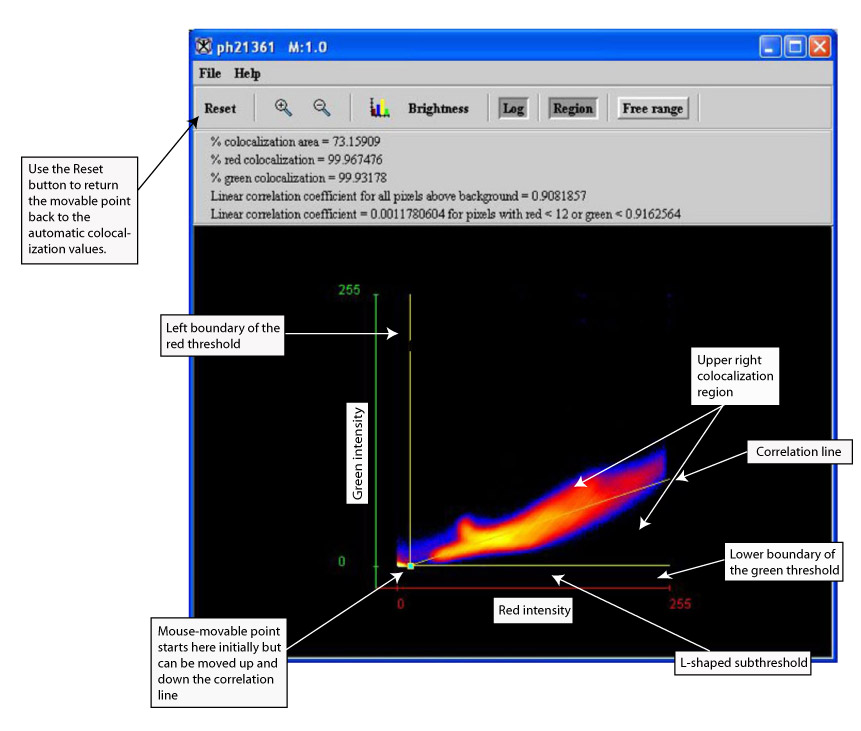
Colocalization histogram window
The Colocalization Histogram window (see Figure 2) contains a 2D histogram with a correlation line and a mouse-movable point on the correlation line. As the point is
|
File
|
Close Colocalization-Closes the colocalization window.
| |
|
Help
|
About Colocalization-Displays online help for this window.
| |
|
Reset
|
Moves the movable point to the position where the linear correlation coefficient of the L-shaped subthreshold region has gone from negative or zero to positive.
| |
|
Magnify image 2.0X
|
Magnifies the histogram by 2.
| |
|
Magnify image 0.5X
|
Magnify the histogram by one-half.
| |
|
Displays Lookup Table (LUT)
|
Displays the Lookup Table (LUT) dialog box, which allows you to specify the LUT for this histogram.
| |
|
Brightness
|
Displays the Brightness/Contrast dialog box, which allows you to adjust the brightness and contrast in the histogram.
| |
|
Log
|
Toggles the histogram between showing counts and log10 (1 histogram counts). The default is no log function.
| |
|
Region
|
Toggles the histogram between not showing lines and showing the bottom and left lines for the upper right colocalization region. The default is not to show the lines.
| |
moved, the statistics at the top of the frame change to reflect the changed upper right rectangular colocalization region whose lower left corner is selected by the point. The colocalization frame is tied to a version of the source color image or to the versions of the two source black-and-white images, so that only those source image pixels in the upper right colocalization region are visible in the source images.
The percent colocalization area, the percent red colocalization, and the percent green colocalization change with the point location. Each point has a red value = threshold and a green value = secondThreshold. Thus, each point defines an upper right rectangular region characterized by red >= threshold and green >= secondThreshold.
The percent colocalization area is given by 100 times the number of pixels belonging to the upper right rectangular region divided by the number of pixels in the entire image or the selected VOI. If limit colocalization to pixels >= threshold is not selected, the percent red colocalization (refer to Figure 3) is given by 100 times the sum of the red values in the upper right rectangular region divided by the sum of the red values in the image or the selected VOI. The percent green colocalization is given by 100 times the sum of the green values in the upper right rectangular region divided by the sum of the green values in the image or the selected VOI.
Note that only pixels above at least one of the two backgrounds are included in any of the above sums.
If limit colocalization to pixels >= threshold is selected, the percent red colocalization is given by 100 times the sum of the red values in the upper right rectangular region divided by the sum of the red values >= the red threshold in the image or selected VOI. The percent green colocalization is given by 100 times the sum of the green values in the upper right rectangular region divided by the sum of the green values >= the green threshold in the image or selected VOI.