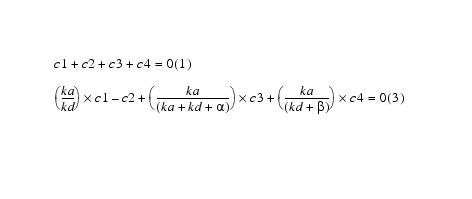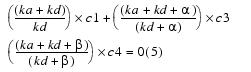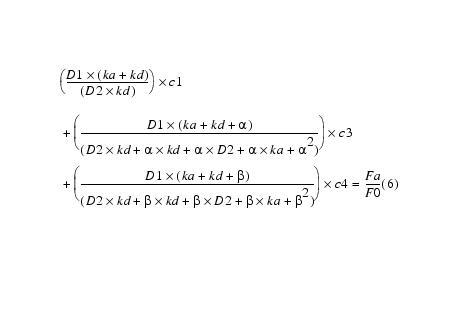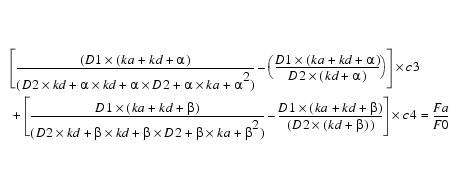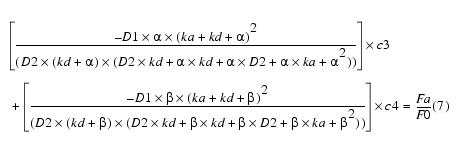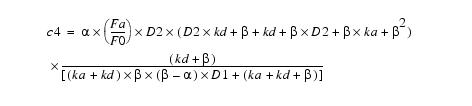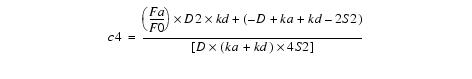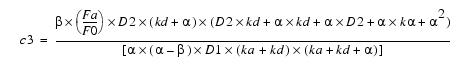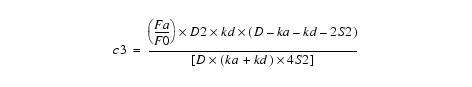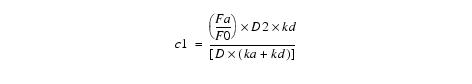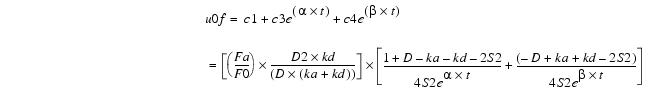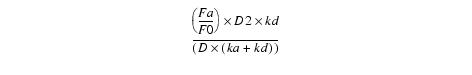Microscopy: FRAP (Fluorescence Recovery After Photobleaching)
This algorithm allows the determination of an association rate, a dissociation rate, and a diffusion transfer coefficient by measuring the recovery of fluorescence in a photobleached area by diffusion from the nonphotobleached surround. The first images in a series of images over time are generally not photobleached. Photobleaching is then used to create a narrow band, small circle, or other small VOI where almost all of the fluorescence is removed.
Contents
- 1 Background
- 2 Applying the FRAP algorithm
- 2.1 To run the FRAP algorithm
- 2.2 To print graphs
- 2.3 To save graphs
- 2.4 To open previously saved graphs
- 2.5 To close graphs
- 2.6 To change the appearance of the graph window
- 2.7 To change the displayed titles of graphs
- 2.8 To change the background color of graphs
- 2.9 To return the graph window to its default settings
- 2.10 To return the range displayed in the graph window to its default settings
- 2.11 To display legends for functions
- 2.12 To change the appearance of functions
- 2.13 To apply mathematical changes to the functions
Background
The normalized recovery of fluorescence over time t is modeled as <math> bottom + span (1- \Gamma e^{\alpha t} - (1- \Gamma) e^{\beta t}) </math>.
A complete photobleaching would reduce the fluorescence to zero. However, a fluorescence level of bottom rather than zero may be measured after photobleaching. As time approaches infinity, the terms <math> \Gamma e^{\alpha t} </math> and <math> (1- \Gamma) e^{\beta t}) </math> go to zero, and the measured fluorescence approaches bottom plus span, which is the mobile fraction.
The algorithm uses curve fitting to determine alpha, beta, gamma, bottom, and span. It then uses alpha, beta, gamma, and the ratio of the photobleached region fluorescence after bleaching to before bleaching to determine the association rate, the dissociation rate, and the diffusion transfer coefficient.
The mathematics of FRAP is based on compartmental modeling in which the compartments must be homogeneous. That is, the fluorescence within a compartment must not have a spatial gradient. If a compartment is not homogeneous, the algorithm cannot be used. More advanced algorithms must then be used to divide the compartments into multiple compartments or introduce partial differentials with respect to distance.
As an option, you may choose to perform registration before running the FRAP algorithm. During the registration, MIPAV registers slices to the first slice after photobleaching. Although the default cost function is correlation ratio, you can select instead least squares, normalized cross correlation, or normalized mutual information. By default the registered image appears in a frame.
| Note: MIPAV runs FRAP on the registered image rather than on the original image. |
The algorithm uses only one color in a color image. If a color image is registered, the registration is based only on this selected color, but all colors in the registered image undergo the same transformation.
| Recommendation: Because registration takes far more time than the FRAP calculation, if more than one FRAP calculation is a possibility, save the registered image to use in future FRAP calculations. |
For images that have a photobleached narrow band with two neighboring unbleached regions, MIPAV uses the equations described in Using FRAP and Mathematical Modeling to Determine the In Vivo Kinetics of Nuclear Proteins by Carrero, McDonald, et al. (refer to "References"). Similar equations were derived for images that have a photobleached circle inside an unbleached region, and solutions were also implemented for the pure 1D diffusion case and for the single exponential model.
To perform FRAP on an image, you select Algorithms >Microscopy >FRAP. The Fluorescence Recovery after Photobleaching dialog box appears. The first task is to delineate the following VOIs on the image:
- A red required photobleached VOI
- A green required whole organ VOI
- An optional blue background VOI
In delineating VOIs for FRAP, it is not necessary to select the New VOI icon. The procedure is to simply select the Add required photobleached VOI option on the FRAP dialog box and then, after selecting an Ellipse, Rectangle, Polyline, or Levelset icon in the VOI toolbar in the MIPAV window, draw the VOI on the image. The required photobleached VOI appears in red on the image.
You return to the FRAP dialog box to create the next required VOI: the whole organ VOI. Select the appropriate option on the FRAP dialog box-in this case. Add required whole organ VOI-and then select the Ellipse, Rectangle, Polyline, or Levelset icon in the VOI toolbar and draw the VOI on the image. This VOI appears in green on the image.
As an option, you can create a third VOI by selecting Add optional background VOI on the FRAP dialog box and repeating the previous steps for drawing the VOI, which appears in blue, on the image.
|
Note: You must create these VOIs on the image after the Fluorescence Recovery after Photobleaching (FRAP) dialog box appears using the instructions provided in the section on [MicroscopyFRAP.html#wp1121763 "Applying the FRAP algorithm" ]. VOIs created outside the dialog box may not have the right colors. |
The VOIs must all have curves present in the first slice after photobleaching (there is no reason to put curves in any other slice). As it runs, the algorithm propagates the photobleached and whole organ VOIs to the other image slices. The background VOI is not propagated to other slices. The photobleached VOI should be contained within the whole organ VOI. The whole organ region has a greater average intensity than the photobleached region, and the optional background region has a smaller average intensity than the photobleached region.
The algorithm uses the average of the background VOI from the first slice after photobleaching to obtain the background constant, which is subtracted from the photobleached intensity and whole organ intensity measurements. It then obtains the ratio Fa/F0, in which Fa is the first slice after photobleaching and F0 is the slice just before photobleaching.
Even with low illumination during the recovery phase, fluorescence loss through photobleaching is expected to occur over the course of the recovery curve. For this loss the time that matters is the exposure time for each slice picture and not the absolute time at which the exposure was made. Since the exposure time for each slice is the same, the time here is proportional to the number of slices. The background corrected photobleached values are divided by the background corrected whole organ values to correct for this loss of fluroescence.
The algorithm then normalizes the values of the (corrected photobleached/ corrected whole organ) by dividing by the value of this ratio just before photobleaching. These normalized photobleached ratios are fitted to a slightly modified version of equation 19 in the Carrero article: <math> R(t, \alpha, \beta, \Gamma) = bottom + span (1 - \Gamma e^{\alpha t} - (1 - \Gamma) e ^{\beta t}) </math> with <math> 0> \alpha > \beta </math> and <math> 1 \ge \Gamma \ge 0 </math> .
The mobile fraction equals bottom span. In this curve fitting the time used is the time elapsed since photobleaching. Alpha, beta, gamma, and the ratio of the whole organ region fluorescence after bleaching to before bleaching are output. The dissociation rate, the association rate, and the diffusion transfer coefficient are obtained from alpha, beta, gamma, and the afterBeforeRatio.
For narrow band 2D, the effective diffusion coefficient in micrometers2 per second is found from the diffusion transfer coefficient. The software measures the photobleached width w as the minimum dimension of the photobleached VOI bounding box and measures the whole organ length l along the same direction.
<math> D_eff = diffusion transfer coefficient (w) \frac {(l-w)} {4.0} </math>
For 1D pure diffusion fitting, the following equation applies:
Equation 1
<math>
I(t) = I_{final} \left ( 1 - \frac {w^2} {\left ( \sqrt {w^2 + 4 \pi t D_{eff}}\right ) } \right )
</math>
where
- t is time
- I is the photobleached fluorescent intensity
- w is the width of the bleaching along the membrane in micrometers (um)
- Deff is the effective 1D diffusion to coefficient in micrometers2 per second
Fitting data for the above equation solves for <math> \frac {D_{eff}} {w^2} </math>.
Then:
<math> D_{eff} = \frac {D_{eff}} {w^2}(p)(p) </math>
You can select an optional check box on the FRAP dialog box to double check the Gauss-Newton nonlinear fitting results with a simple grid search pattern. The software calculates the Sum of Squares of Errors (SSE) at every legal point on a grid and then finds the sum of the squares of the fitted photobleached data minus the actual photobleached data for every slice starting with the first slice after photobleaching.
For the 2D narrow band and 2D circle photobleached models, the algorithm uses a 3D grid with 201 alpha points, 201 beta points, and 101 gamma points. It then varies both alpha and beta from 0.05 times the values found in the nonlinear fit to 20 times the values found in the nonlinear fit. It geometrically increments the values so that each value is about 1.03 times as great as the previous value and arithmetically increments gamma by 0.01 from 0 to 1.
The algorithm finds the global SSE minimum and, if present, any local SSE minimums, which are the lowest point in a 5 by 5 by 5 cube. The 3D space is searched with the restriction that beta <= alpha. Points with beta > alpha are not included in the 3D search and are simply filled in with SSE values equal to 1.1 times the SSE maximum found over the permissible space. The search is conducted with the bottom and span values kept fixed at the values found by the nonlinear fit. Since these values are very likely to have been accurately determined, this should not be a problem. In any event a search over a 5D space would be very time consuming. A 201 by 201 by 101 3D error image is created to display the calculated SSE values. The error image name is the source image name with _err appended on the end.
Point VOIs appear at the locations of the global minimum and at local minimums if any exist. The algorithm stores point VOIs in a folder titled defaultVOI_sourceImageName_err. For the pure 1D fit and the single exponential fit, the search is simply one dimensional; therefore, the software does not create an error image. For the pure 1D fit, <math>
201 \frac {D_{eff}} {w^2}
</math> values going from 0.05 times the nonlinear fit value to 20 times the nonlinear fit value are used to calculate SSE. For the single exponential fit, ![]() half values going from 0.05 times the nonlinear fit value to 20 times the nonlinear fit value are used to calculate sse.
half values going from 0.05 times the nonlinear fit value to 20 times the nonlinear fit value are used to calculate sse.
In the derivation for the case in which the photobleached area is a circle, there are only two compartments:
- 0, the inside of the circle
- 1, the outside of the circle
The equations are:
Equation 2
<math>
\frac {\partial u_0f} {\partial t} = -D_1 (u_0f) + D_2 (u_1f) - ka (u_0f) + kd (u_0b)
</math>
<math> \frac {\partial u_1f} {\partial t} = D_1 (u_0f) - D_2 (u_1f) - ka (u_1f) + kd (u_1b) </math>
<math> \frac {\partial u_0b} {\partial t} = ka (u_0f) - kd (u_0b) </math>
<math> \frac {\partial u_1b} {\partial t} = ka (u_1f) - kd (u_1b) </math>
<math> D_1 = \left ( \frac {F_a} {F-a +F_0 - F_a} \right ) D_t = \left ( \frac {F_a} {F_0} \right )D_t </math>
<math> D_2 = \left ( \frac {(F_0 - F_a)} {(F_a + F_0 - F_a)} \right ) D_t = \left ( \frac {(F_0 - F_a)} {F_0} \right ) D_t </math>
As expected
<math> D_1 + D_2 = D_t </math>
<math> u = (u_0f, u_1f, u_0b, u_1b) </math>
<math> u_0 = (0, \left ( \frac {k_d} {(k_a + k_d)} \right ) \left ( \frac {F_a} {F_0} \right ), 0, \left ( \frac {k_a} {(k_a + k_d)} \right ) \left ( \frac {F_a} {F_0} \right )) </math> The eigenvalues are found by setting the determinant to zero (0):
Equation 3
<math>
\begin{bmatrix}
{-D_1-ka-e} & D_2 & kd & 0\\
D_1 & {-D_2 -ka -e} & 0 & kd\\
ka & 0 & {-kd -e} & 0\\
0 & ka & 0 & {-kd -e}
\end{bmatrix}
</math>
This gives the equation:
<math> e^4 + (D_1 +D_2 +2ka +2kd)e^2 +(D_1(ka) +2D_1(kd) + D_2(ka) +2D_2 (kd) + ka^2 + 2ka(kd) + kd^2(e^2) +D_1 (ka) (kd) + D_1(kd^2) + D_2 (ka)(kd) + D_2 (kd^2))e = 0 </math>
Using D1 D2 = D, the above equation factors as:
<math> e(e+ka + kd) (e^2 + (D+ka+kd) (e+D(kd))) = 0 </math>
The quadratic gives the roots alpha and beta with
<math> \alpha = -s_1 + s_2 </math>
<math> \beta = -s_1 - s_2 </math>
where
<math> S_1 = \frac {(D+ka +kd)} {2} </math>
<math> s_2 = \frac {\sqrt {((D + ka+kd)^2 -4D(kd))}} {2} </math>
The eigenvalue <math> e = 0 </math> gives the eigenvector:
<math> 1 </math>
<math> \left ( \frac {D_1}{D_2} \right ) </math>
<math> \left ( \frac {ka} {kd} \right ) </math>
<math> \left ( \frac {D_1ka} {D_2kd} \right ) </math>
The eigenvalue <math> e = -ka-kd </math> gives the eigenvector:
<math> 1 </math>
<math> \left ( \frac {D_1} {D_2}\right ) </math>
<math> -1 </math>
<math> - \left ( \frac {D_1} {D_2}\right ) </math>
The eigenvalue <math> e = \alpha </math> gives the eigenvector:
<math> 1 </math>
<math> \frac {D_1 (kd + \alpha)} {D-2(kd) + \alpha (kd) + \alpha (D_2) + \alpha (ka) + \alpha^2} </math>
<math> \frac {ka} {kd+\alpha} </math>
<math> \frac {D_1 (ka)} {D-2(kd) + \alpha (kd) + \alpha (D_2) + \alpha (ka) + \alpha^2} </math>
The eigenvalue <math> e = \beta </math> gives the eigenvector:
<math> 1 </math>
<math> \frac {D_1(kd + \beta)} {D_2kd + \beta (kd) + \beta (D_2) + \beta (ka) + \beta^2} </math>
<math> \frac {D_1(ka)} {D_2kd + \beta (kd) + \beta (D_2) + \beta (ka) + \beta^2} </math>
Let the eigenvectors be v1, v2, v3, and v4. Let the matrix V be given by:
<math> \begin{bmatrix} v11 & v21 & v31 & v41\\ v12 & v22 & v32 & v42\\ v13 & v23 & v33 & v43\\ v14 & v24 & v34 & v44 \end{bmatrix} </math>
Let the vector C be
<math> \begin{bmatrix} c1\\ c2\\ c3\\ c4 \end{bmatrix} </math>
Remembering that <math> u_0 </math> is the vector of initial conditions, we wish to solve:
<math> VC = u_0 </math>
Adding equations 1 and 3:
yields equation 5:
Equation 4
Adding equations 2 and 4:
Equation 5yields equation 6:
Multiplying 5 by ![]() and adding to 6 yields:
and adding to 6 yields:
which simplifies to:
Equation 8Multiplying equation 1 by ![]() and adding to equation 2 yields:
and adding to equation 2 yields:
Equation 9
Multiplying equation 8 by ![]() and adding to equation 7 yields:
and adding to equation 7 yields:
This simplifies to:
Equation 11Substituting c4 back into equation 8 yields c3:
Equation 12This simplifies to:
Equation 13Putting c3 and c4 in equation 5 and solving for c1 yields:
Equation 14Putting c1, c3, and c4 into equation 4 and solving for c2 yields c2 = 0.
Thus, the solution is:
Equation 15The above equation is normalized by dividing by
Equation 16The coefficient of exp(alpha*t) in the normalized equation equals -gamma so ![]() and the normalized equation can be written as:
and the normalized equation can be written as:
Image types
You can apply this algorithm to both color and black-and-white 3D images. However, with color images, the algorithm uses only one of the colors.
Special notes
This algorithm can only be used when the fluorescence is homogeneous in a compartment. If the fluorescence has spatial gradients across a compartment, a model using partial derivatives with respect to distance should be employed.
References
Axelrod, D., D. E. Koppel, J. Schlessinger, E. Elson, and W. W. Webb. "Mobility Measurement by Analysis of Fluorescence Photobleaching Recovery Kinetics." Biophysical Journal 16 (1976):1055-1069.
Carrero, Gustavo, Darin McDonald, Ellen Crawford, Gerda de Vries, and Michael J. Hendzel. "Using FRAP and Mathematical Modeling to Determine the In Vivo Kinetics of Nuclear Proteins." Methods 29 (2003):14-28.
Lippincott-Schwartz, J., J. F. Presley, K. J. M. Zaal, K. Hirschberg, C. D. Miller, and J. Ellenberg. "Monitoring the Dynamics and Mobility of Membrane Proteins Tagged with Green Fluorescent Protein." Methods in Cell Biology 58 (1999):261-281.
Phair, Robert D. "Practical Kinetic Modeling of Large Scale Biological Systems." http://www.bioinformaticsservices.com/bis/resources/cybertext/IBcont.html.
Applying the FRAP algorithm
This section explains how to run the FRAP algorithm and how to modify the appearance of the resulting graph windows.
To run the FRAP algorithm
- Open a 3D color or 3D black-and-white image.
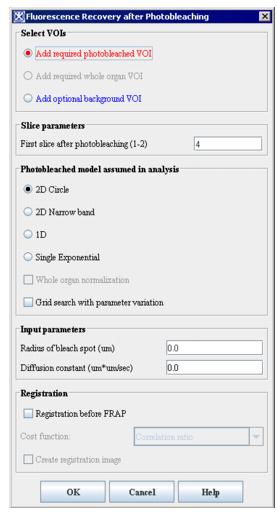
- Select Algorithms > Microscopy > FRAP. The Fluorescence Recovery after Photobleaching dialog box (see Figure 1) opens.
Figure 1. Fluorescence Recovery after Photobleaching dialog boxAdd required photobleached VOIApplies a mandatory photobleached VOI, which appears in red, to the first image slice after photobleaching. Make sure that the VOI delineates the photobleached area. By default, this radio button is selected.Add required whole organ VOIAdds a mandatory whole organ VOI, which appears in green, to the first image slice after photobleaching. This VOI should contain the entire photobleached VOI and should be brighter than the photobleached VOI.All optional background VOIAdds an optional background VOI, which appears in blue, to the first image after photobleaching. This VOI should delineate a featureless area that is darker than the photobleached area.Color selection (only appears for color images)Select one of the available colors-red, green, or blue-listed that corresponds to the fluorescence undergoing photobleaching. By default, red is selected. However, if red is single valued, the default is green.First slice after photobleachingType the slice number of the first slice after photobleaching. If the image's file header contains this information, the slice number appears. Otherwise, the default is 4.2D narrow bandAssumes a narrow photobleached band surrounded by a large unbleached region on each side. Unless a photobleached region circle is found in the file header, the default value is 2D narrow band.2D circleAssumes a small circle in the midst of a large unbleached region. If the file header for the image contains information that the photobleached region is a circle, the default is 2D circle.1DAssumes pure 1D diffusion.Single exponentialAssumes recovery according to a single exponential.Grid search with parameter variationConducts a double check by grid search.Registration before FRAPRegisters the image slices that are not aligned. Select this item so that slice alignment occurs before FRAP. The default is no registration.Cost functionSpecifies the registration cost function. You may select correlation ratio (the default), least squares, normalized cross correlation, or normalized mutual information. To use this item, you must first select Registration before FRAP.Create registration imageCreates the registered image in a separate image window. To use this item, you must first select Registration before FRAP. By default, this item is selected.OKApplies the algorithm according to the specifications made in the dialog box.CancelDisregards any changes that you made in the dialog box and closes this dialog box.HelpDisplays online help for this dialog box.
- Select for color images the fluorescence color in the Color selection panel.
Note: Only the color that you select has a role in the FRAP mathematics.
- Read to see, if an information panel is present, if either the shape of the photobleached region or the first slice after photobleaching is specified.
- Go to the MIPAV window and adjust the image slice slider to display the first slice after photobleaching.
- Type the number of the first slice after photobleaching in the text box in the Slice parameters panel.
Remember: The slice number appears on the title bar of the image window. As you move the image slice slider in the MIPAV window to the right, the slice number increases. As you move it to the left, the slice number decreases.
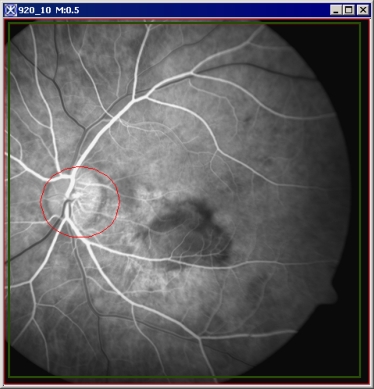
- Select Add required photobleached VOI in the Select VOIs panel in the FRAP dialog box.
- Go to the MIPAV window, and select one of these icons from the VOI toolbar:
- Draw the VOI on the image. The VOI appears in red.
Note: In drawing these VOIs, you do not need to first select the New VOI icon.
- Select Add required whole organ VOI in the Select VOIs panel in the FRAP dialog box.
- Create a whole organ VOI by selecting
 ,
,  ,
,  , or
, or  to draw a rectangle, ellipsoidal, polygon/polyline, or levelset VOI on the image around the whole organ region in the first slice after the photobleaching. A green VOI appears on the image.
to draw a rectangle, ellipsoidal, polygon/polyline, or levelset VOI on the image around the whole organ region in the first slice after the photobleaching. A green VOI appears on the image.
Whole organ region: The whole organ region should entirely contain the photobleached region and be brighter than the photobleached region.
- Go to the next step, or, if you wish, create an optional background VOI using the following directions:
- Select Add optional background VOI in the Select VOIs panel in the FRAP dialog box.
- Go to the MIPAV window and select
 ,
,  ,
,  , or
, or  to draw a rectangle, ellipsoidal, polygon/polyline, or levelset VOI on the image around the background region in the first slice after the photobleaching. A blue VOI appears on the image.
to draw a rectangle, ellipsoidal, polygon/polyline, or levelset VOI on the image around the background region in the first slice after the photobleaching. A blue VOI appears on the image.
Background region: The background region should not contain any structures and should be darker than the photobleached region. - Register the image slices as an option by doing the following:
- Select Registration before FRAP.
- Select a cost function in the Cost function list. Although correlation ratio is the default cost function, you can also select least squares, normalized cross correlation, or normalized mutual information.
- Select or clear Create registration image. Since registration is far more time consuming than calculating FRAP, selection is the default.
- Select the photobleached model assumed in analysis:
- 2D narrow band
- 2D circle
- 1D
- Single exponential
- Select Grid search with parameter variation if you want to double check the nonlinear fitting engine with a grid search.
- Click OK.
- The algorithm begins to run and a progress bar appears with the status. When the algorithm finishes running, the progress bar disappears, and the following windows appear
-
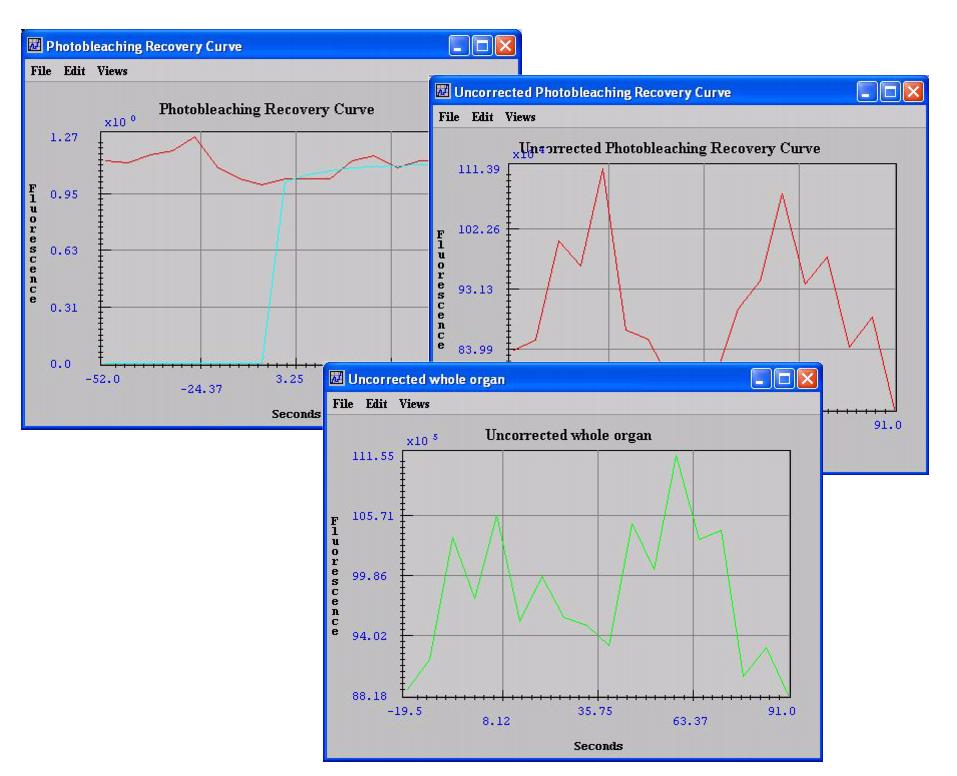
- Photobleaching Recovery Curve window (see Figure 3), which displays a graph of the fitting of the normalized photobleached region recovery curve (the calculated parameters appear on the Data page of the Output window)
|
File
|
Open Graph (Ctrl0)-Allows you to open a previously saved graph. When you select this command, the Open Graph Data dialog box appears.
| |
|
Save Graph (CtrlS)-Allows you to save a graph as a .PLT file. When you select this command, the Save dialog box appears.
| ||
|
Print Graph (CtrlP)-Allows you to print the graph. When you select this command, the Print dialog box appears.
| ||
|
Close Graph (CtrlX)-Closes the graph immediately.
| ||
|
Edit
|
Delete Function-Allows you to delete a specified function on the graph unless the graph contains only one function.
| |
|
Copy Function-Allows you to copy the function that you specify.
| ||
|
Paste Function-Allows you to paste a previously copied function to the graph.
| ||
|
Views
|
Modify Graph Features-Allows you to change all of the graph features, such as the names and colors of the functions, the background color of the graph, the ranges used, whether the gridlines appear, and so on. When you select this command, the Modify Graph window opens.
| |
|
Reset Range to Default-Changes the range displayed in the graph to the default range.
| ||
|
Reset Graph to Original-Changes the range displayed in the graph to the original range.
| ||
|
Graph
|
Displays the amount of fluorescence over time (seconds).
| |
- Uncorrected Photobleaching Recovery Curve window (see Figure 3)
- Uncorrected Whole Organ window (see Figure 3)
- If you selected Create registration image in the FRAP dialog box, an image window with a registered source image appears.
| Note: All of the three graph windows-the Photobleaching Recovery Curve, Uncorrected Photobleaching Recovery Curve, and Uncorrected Whole Organ windows-have the same menus and commands that work in the same way. |
- If you selected Grid search with parameter variation in the FRAP dialog box and either 2D narrow band or 2D circle, a 201 by 201 by 101 3D error image is created to display the sum of squared error values.
To print graphs
In a graph window:
- Select File > Print, or press Ctrl P on the keyboard. A Print dialog box (see Figure 4) appears.
- Select the printer, print range, and number of copies.
- Click OK.
To save graphs
- Select File > Save, or press Ctrl S on the keyboard. The Save dialog box appears.
- Select a directory in which to store the graph.
- Type a name for the graph, including the .PLT extension, in the File Name box.
- Click OK.
To open previously saved graphs
- Select File > Open, or press Ctrl O on the keyboard. The Open dialog box appears.
- Navigate to the directory where the graph is stored.
- Select the name of the graph.
- Click OK.
To close graphs
Select File > Close, or press Ctrl X on the keyboard. The graph window closes.
To change the appearance of the graph window
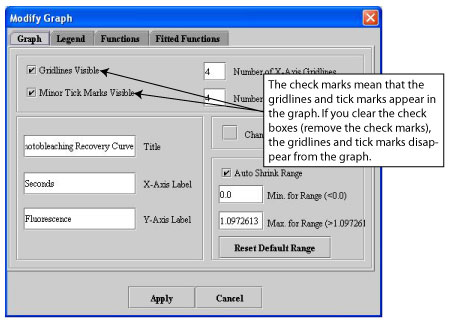
Using the Modify Graph Features command on the Views menu of each of the graph windows, you can change how the data appears in each graph. When you select Views > Modify Graph Features, the Modify Graph dialog box opens.
The Modify Graph dialog box (see Figure 6) allows you to change the following:
- The appearance of the graph
- Whether legends for functions appear on the graph
- The color and visibility of functions and whether points appear on the functions
- Mathematical adjustments to the functions
To change the displayed titles of graphs
Changing the title of graphs is very easy.
- Select Views > Modify Graph Features in the graph window. The Modify Graph Features dialog box opens.
- Type the new title in Title. You can simply type over the current title of the graph.
- Click Apply.
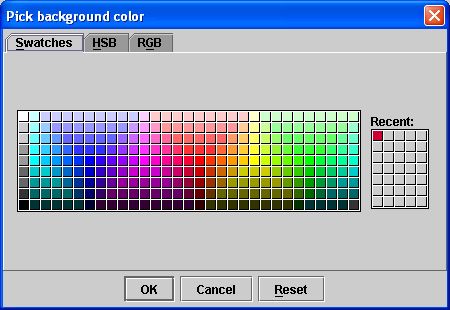
To change the background color of graphs
- Select Views > Modify Graph Features in the graph window. The Modify Graph dialog box opens.
- Click Change background color on the Graphs page. The Pick Background Color dialog box (see Figure 7) opens.
- Select a color on the one of the pages in the dialog box: Swatches, HSB, or RGB page.
- Click OK. The Pick Background Color dialog box closes.
- Click Apply. The Modify Graph dialog box closes. The background of the graph window should now be the color you selected.
Figure 7. Pick Background Color dialog boxChange background colorAllows you to change the background color of the grid. By default, the background color is light gray. When you click this button, the Pick Background Color dialog box opens.Auto shrink rangeAllows you to adjust the display of the Y axis of the graph. By default, this check box is selected.Minimum for rangeSpecifies the minimum value for the Y axis, which must be 0.0 or less. The default value is 0.0.Maximum for rangeSpecifies the maximum value for the X axis, which must be 1.0 or more. The default value is 1.0.Reset default rangeReinstates the default range for the graph, which means that the value of Minimum for range returns to 0.0 and the value for Maximum for range returns to 1.0.ApplyApplies immediately the changes to the graph according to the specifications in this dialog box but keeps this dialog box open.CancelDisregards any changes that you made in the dialog box and closes this dialog box.HelpDisplays online help for this dialog box.To return the graph window to its default settings
If you made changes in the way a graph appears in the Modify Graph dialog box and now would like to return to the default settings, select in the graph window View > Reset Graph to Original or press Ctrl Z on the keyboard.
To return the range displayed in the graph window to its default settings
The Modify Graph dialog box allows to change the range that is displayed in a graph window. If, after modifying the range, you want to reinstate the minimum and maximum values in the range for a graph, do either of the following:
In the graph window
Select Views > Reset Range to Default.
In the Modify Graph dialog box
- Select Views > Modify Graph Features in the graph window. The Modify Graph dialog box opens.
- Select Reset default range.
- Click Apply.
The range returns to its default settings.
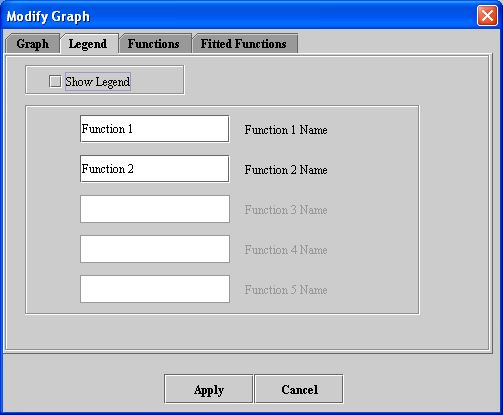
To display legends for functions
- Select Views > Modify Graph Features in the graph window. The Modify Graph dialog box opens.
- Click Legend. The Legend page (see Figure 8) appears.
- Select Show legend.
- Accept or change the names of the functions in the text boxes.
- Click Apply. The legends should appear in the graph window.
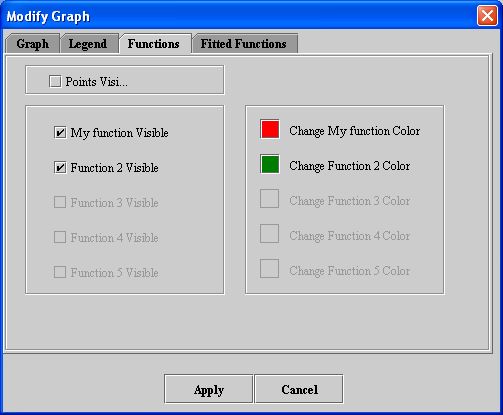
To change the appearance of functions
- Select Views > Modify Graph Features in the graph window. The Modify Graph dialog box appears.
- Click Functions. The Functions page (see Figure 9) appears.
- Select Points visible if you want to display all of the points on the functions.
- Change the color of each function by clicking Change function color.
- Click Apply. In the graph window, the appearance of the functions should display according to your specifications.
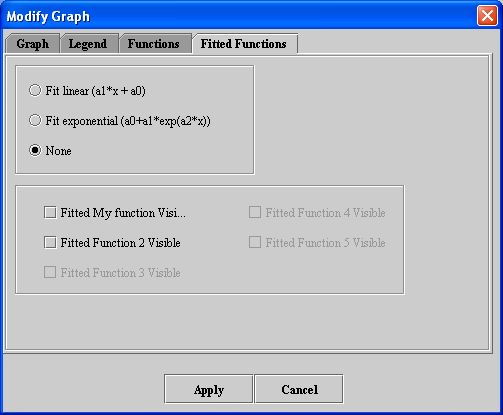
To apply mathematical changes to the functions
- Select Views > Modify Graph Features in the graph window. The Modify Graph dialog box appears.
- Click Fitted Functions. The Fitted Functions page (Figure 10) appears.
- Select Fit linear or Fit exponential. The default choice is None.
- Select the functions to which these changes should be made.
- Click Apply. The functions should change according to your specifications.