Filters (Spatial): Coherence-Enhancing Diffusion
Contents
Summary
Coherence-enhancing filtering is a specific technique within the general classification of diffusion filtering. Diffusion filtering, which models the diffusion process, is an iterative approach of spatial filtering in which image intensities in a local neighborhood are utilized to compute new intensity values.
Coherence-enhancing filtering is useful for filtering relatively thin, linear structures such as blood vessels, elongated cells, and muscle fibers.Two major advantages of diffusion filtering over many other spatial domain filtering algorithms are:
- A' priori image information can be incorporated into the filtering process;
- The iterative nature of diffusion filtering allows for fine grain control over the amount of filtering performed.
There is not a consistent naming convention in the literature to identify different types of diffusion filters. This documentation follows the approach used by Weickert (see "References," below). Specifically, since the diffusion process relates a concentration gradient with a flux, isotropic diffusion means that these quantities are parallel. Regularized means that the image is filtered prior to computing the derivatives required during the diffusion process. In linear diffusion the filter coefficients remain constant throughout the image, while nonlinear diffusion means the filter coefficients change in response to differential structures within the image. Coherence-enhancing filtering is a regularized nonlinear diffusion that attempts to smooth the image in the direction of nearby voxels with similar intensity values.
Background
All diffusion filters attempt to determine the image ![]() that solves the well-known diffusion equation, which is a second-order partial differential defined as
that solves the well-known diffusion equation, which is a second-order partial differential defined as
<math> \partial_tI = div(D\triangledown I) </math>
where
The quantity that distinguishes different diffusion filters is primarily the diffusion tensor also called the diffusivity.
In homogeneous linear diffusion filtering, the diffusivity, D, is set to 1 and the diffusion equation becomes: <math> \partial_tI = \partial_{xx}I +\partial_{yy}I </math>
In isotropic nonlinear diffusion filtering, the diffusivity term is a monotonically decreasing scalar function of the gradient magnitude squared, which encapsulates edge contrast information. In this case, the diffusion equation becomes:'
<math> \partial_tI = div (D(\left | \triangledown I \right |^2) \triangledown I </math>
It is well known that derivative operations performed on a discrete grid are an ill-posed problem, meaning derivatives are overly sensitive to noise. To convert derivative operations into a well-posed problem, the image is low-pass filtered or smoothed prior to computing the derivative. Regularized isotropic (nonlinear) diffusion filtering is formulated the same as the isotropic nonlinear diffusion detailed above; however, the image is smoothed prior to computing the gradient. The diffusion equation is modified slightly to indicate regularization by including a standard deviation term in the image gradient as shown in the following equation:
<math> \partial_tI = div (D(\left | \triangledown I_\sigma \right |^2) \triangledown I_\sigma </math>
The smoothing to regularize the image is implemented as a convolution over the image and therefore this filtering operation is linear. Since differentiation is also a linear operation, the order of smoothing and differentiation can be switched, which means the derivative of the convolution kernel can be computed and convolved with the image resulting in a well-posed measure of the image derivative.
In edge-enhancing anisotropic diffusion, the diffusivity function allows more smoothing parallel to image edges and less smoothing perpendicular to these edges. This variable direction smoothing means that the flux and gradient vectors no longer remaining parallel throughout the image, hence the inclusion of the term anisotropic in the filter name. Directional diffusion requires that the diffusivity function provide more information than a simple scalar value representing the edge contrast. Therefore, the diffusivity function generates a matrix tensor that includes directional information about underlying edges. We refer to a tensor-valued diffusivity function as a diffusivity tensor. In edge-enhancing anisotropic diffusion, the diffusivity tensor is written as the following: <math> (D \left ( \triangledown I_\sigma \right )= D( \triangledown I_\sigma \triangledown I^T_\sigma) </math>
Directional information is included by constructing an orthonormal system of eigenvectors ![]() of the diffusivity tensor so that
of the diffusivity tensor so that ![]() and
and ![]() .
.
Coherence-enhancing anisotropic diffusion is an extension of edge-enhancing anisotropic diffusion that is specifically tailored to enhance line-like image structures by integrating orientation information. The diffusivity tensor in this case becomes:
In this diffusivity tensor, ![]() is a Gaussian kernel of standard deviation
is a Gaussian kernel of standard deviation ![]() , which is convolved (
, which is convolved (![]() ) with each individual component of the
) with each individual component of the ![]() matrix. Directional information is provided by solving the eigensystem of the diffusivity tensor without requiring
matrix. Directional information is provided by solving the eigensystem of the diffusivity tensor without requiring ![]() and
and ![]() .
.
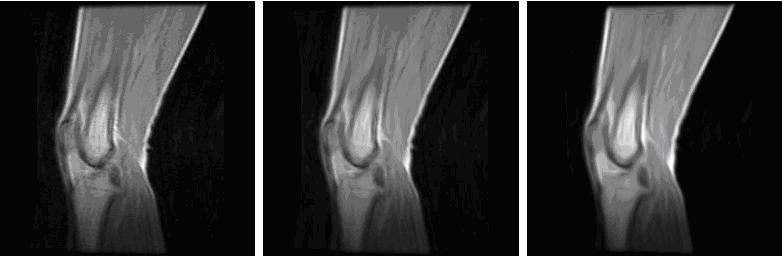
Figure 1 shows the results of applying the coherence-enhancing anisotropic diffusion filter to an example MR knee image.
Image types
You can apply this algorithm to all data types except complex and to 2D, 2.5D, and 3D images.
Special notes
The resulting image is, by default, a float image.
Applying the Coherence-Enhancing Diffusion algorithm
To run this algorithm, complete the following steps:
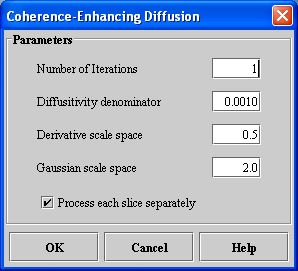
- Select Algorithms > Filter > Coherence-Enhancing Diffusion. The Coherence-Enhancing Diffusion dialog box opens (Figure 2).
|
Number of iterations
|
Specifies the number of iterations, or number of times, to apply the algorithm to the image.
|
|
|
Diffusitivity denominator
|
Specifies a factor that controls the diffusion elongation.
| |
|
Derivative scale space
|
Specifies the standard deviation of the Gaussian kernel that is used for regularizing the derivative operations.
| |
|
Gaussian scale space
|
Specifies the standard deviation of the Gaussian filter applied to the individual components of the diffusivity tensor.
| |
|
Process each slice separately
|
Applies the algorithm to each slice individually. By default, this option is selected.
| |
|
OK
|
Applies the algorithm according to the specifications in this dialog box.
| |
|
Cancel
|
Disregards any changes that you made in this dialog box and closes the dialog box.
| |
|
Help
|
Displays online help for this dialog box.
| |
- Complete the fields in the dialog box.
- When complete, click OK.
- The algorithm begins to run, and a status window appears. When the algorithm finishes, the resulting image appears in a new image window.
References
- Weickert, Joachim. "Nonlinear Diffusion Filtering," in Handbook of Computer Vision and Applications, Volume 2, eds.
- Bernd Jahne, Horst Haussecker, and Peter Geissler. (Academic Press, April 1999), 423-450.
- Weickert, Joachim. Anisotropic Diffusion in Image Processing (Stuttgart, Germany: Teubner, 1998).