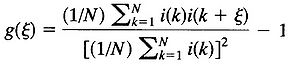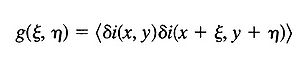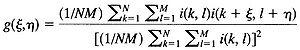Autocovariance Coefficients
Autocovariance is a measure of the degree to which the outcome of the function f (T + t) at coordinates (T+ t) depends upon the outcome of f(T) at coordinates t. It provides a description of the texture or a nature of the noise structure
Contents
Background
In statistics, given a real stochastic process f(t), the auto-covariance is simply the covariance of the signal against a time-shifted version of itself. If each state of the series has a mean:
<math> E=[f(T)]=\mu_T </math>
Then the auto-covariance is given by the following equation:
<math> G_{xx}(T,S)=E[(f_T - \mu_T)*(f_S - \mu_S)]=(E(f_T * f_S) - (\mu_T - \mu_S)) </math>
If f(t) is wide sense stationary function, then
<math> \mu_T = \mu_S = \mu </math>
And for all T and S
<math> G_{xx} (T,S)=G_{xx}(S-T)=G_{xx}(t) </math>
Where t=S-T is the amount of time by which the signal has been shifted.
When normalized by the variance <math>\sigma^2</math> the auto-covariance function becomes the auto-covariance coefficient:
<math> \rho = G_{xx}(t)/\sigma^2 </math>
Calculation of the auto-covariance function G(t) of a randomly varying function i(T) may be done in the time domain using the following equation:
<math> G(t) = \left \langle (i(T) * i(t+t) \right \rangle </math>
Where, the <> brackets indicate integration over time.
Correspondingly, the auto-covariance function may be calculated in the spatial domain, as
<math> g(\xi)=\delta_i (x) * \delta_i (x+\xi) </math>
<math> \delta_i = \frac{(i(T)- <(i(T)>}{<i(T)>} </math>
Where, the <> brackets indicate integration over time.
This gives us the normalized auto-covariance function or auto-covariance coefficient:
<math>
g(t)= \left \langle \sigma_i (T) * \sigma_i (T+t)\right \rangle = [i(T) * i(T+t) - \left \langle i(T)\right \rangle ^2] / \left \langle i(T)\right \rangle ^2 = [G(t)/\left \langle i(T)\right \rangle ^2] -1 </math>
When the data consist of a set of N discrete points, the averaging is performed as sums, then in spatial domain the 1D auto-covariance function is calculated by
If the random intensity variable, i, is a function of two independent variables, x and y, then, it is possible to define a corresponding two-dimensional auto-covariance function:
For a discrete set of data this becomes:
Notes
While some medical literature refers to this algorithm as an autocorrelation, it is actually an auto-covariance since means are subtracted.
An auto-covariance function, which falls rapidly as a function of t, indicates that the resultant noise is in actual fact independent except at short separated distances, providing an appearance of 'sharp' noise.
An auto-covariance function, which falls off slowly and smoothly as a function of t, indicates that the noise is highly correlated. At a given point, a positive value of the auto-covariance means that the noise tends to be of the same sign, while a negative value indicates that the noise tends to be of the opposite sign.
In short, the amplitude of the auto-covariance at zero displacement provides a measure of the noise magnitude, while the shape the auto-covariance can be used to describe the nature of noise.
Image types
Color and black and white 3D and 4D images.
Applying Autocovariance Coefficients
To use this algorithm, do the following:
- Select Algorithms > AutoCovariance Coefficients in the MIPAV window. The AutoCovariance Coefficients dialog box appears.
- Click OK. The algorithm begins to run, and a status bar appears with the status. When the algorithm finishes running, the progress bar disappears, and the results replace the original image.
References
Digital Image Processing, Second Edition by Rafael C. Gonzalez and Richard C. Woods, Prentice-Hall, Inc., 2002, pp. 205 - 208 and pp. 414-417.
"Two-photon image correlation spectroscopy and image cross-correlation spectroscopy" by P. W. Wiseman, J.A. Squier, M.H. Ellisman, and K.R. Wilson, Journal of Microscopy, Vol. 200. Pt. 1, October 2000, pp. 14-25.
"Quantitation of Membrane Receptor Distributions by Image Correlation Spectroscopy: Concept and Application" by Nils O. Petersen, Pia L. Hoddelius, Paul W. Wiseman, Olle Seger, and Karl-Eric Magnusson, Biophysical Journal, Volume 65, September, 1993, pp. 1135-1146.
"Image cross-correlation spectroscopy: A new experimental bipohysical approach to measurement of slow diffusion of fluorescent molecules" by Mamta Srivastava & Nils O. Petersen, Methods in Cell Science, Vol. 18, March, 1996, pp. 47-54.
"Analysis of recorded image noise in nuclear medicine" by Benjamin M. W. Tsui, Robert N. Beck, Kunio Doi and Charles E. Metz, Phys. Med. Biol., 1981, Vol. 26. No. 5, 883-902. Printed in Great Britain.