Registration: Landmark-TPSpline

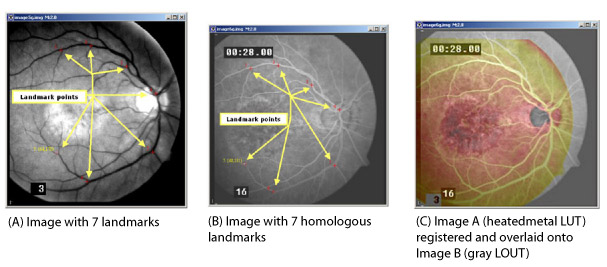
The Landmark-TPSpline (Thin Plate Spline) algorithm allows you to align two or more images along a corresponding VOI that you delineate in all of the images.

When applied to 2D images, the Landmark-TPSplines algorithm uses a 2D interpolation scheme for arbitrarily spaced tabulated data (x'i',y'i',f(x'i',y'i)). These splines are the generalization of the natural cubic splines in 1D. The spline surface represents a thin metal sheet that is constrained not to move at the grid points. When applied to 3D images, the TPSplines algorithm operate on data of the form (x'i',y'i',z'i',f(x_i,y_i,z_i).

MIPAV uses the spline matching points sets to obtain spline interpolation coefficients, which it uses to transform all the xorg,yorg grid positions in the base image space to xne w, ynew grid positions in the match space. Then, at every xorg,yorg grid position in the base space, MIPAV checks to see if the corresponding xnew,ynew grid position in the match space is within the image bounds of the match image.

If xnew 'and' ynew is within the match space bounds, then the data value at the xnew,ynew grid position in the match space is assigned to be the registered value at the xorg,yorg position in the base space. Since xnew, ynew is a floating point number and the data in the match image is only contained at integer grid points, interpolation must be used.

For a 2D image, the data value at xnew,ynew in the match space is obtained by bilinear interpolation from its four nearest neighbors. For a 3D image, the data value at xnew,ynew in the match space is obtained by trilinear interpolation from its eight nearest neighbors. If the xnew, ynew is outside the match space bounds, then a zero is assigned to the xorg, yorg position in the base space.

When processing the image, the algorithm first computes the thin plate spline coefficients and then generates match space grid positions from base space grid positions.

Figure 1. Example of Registration: Landmark-TPSpline algorithm

You can apply this algorithm to all 2D and 3D image types. The dimensions or image type of the match image need not be the same as the dimensions or image type of the base image. The registered image has the same image type as the match image and the same extents as the base image.

The following notes apply:

• For 2D images, three or more points are required. The algorithm may fail if nearly all of the points fall on the same line.
• For 3D images, four or more points are required and the algorithm may fail if the points nearly all fall on the same plane.

Refer to the following references for more information about this algorithm:

David Eberly, "Thin Plate Splines" of Magic Software at http://www.magic-software.com. Also at the same site are the files: MgcInterp2DThinPlateSpline.h, MgcInterp2DThinPlateSpline.cpp, MgcInterp3DThinPlateSpline.h, MgcInterp3DThinPlateSpline.cpp Paper that explains warping from one x,y source to another x',y target set.

Fred L. BookStein, "Principal Warps: Thin-Plate Splines and the Decompositions of Deformations," IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 11, No. 6, June 1989, pp. 567-585.

To run this algorithm, complete the following steps:

Selected image is a match image, the image that gets transformed until it is registered to the base image.

1. Open two images: a base image and a match image.
2. Perform, as an option, any image processing, such as improving the contrast, eliminating noise, adding color, etc., on both images.
3. Delineate a point VOI on the base image using the point VOI icon and mouse.
4. Select the match image.
5. Delineate a point VOI on the match image at corresponding positions on the image.

   Note: Make sure that you delineate the points on the match image in the same order as on the base image. That is, point 1 on the base image should correspond to point 1 on the match image, point 2 on the base image correspond to point 2 on the match image, and so on.

   
   

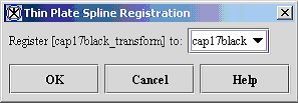
6. Click Algorithm > Registration > Landmark - TPSPline. The Thin Plate Spline Registration dialog box opens.
7. Select the base image in the Register to list box.
8. lick OK. The algorithm begins to run. A pop-up window appears with the status. The following messages appear in succession: "Performing base to match grid transformation" and "Performing interpolation into result buffer." When the algorithm finishes running, the pop-up window closes, and the result appears in a new image window.

   Figure 2. Thin Plate Spline Registration dialog box

   Register to	Displays a list of images including the base image and any match images.
   OK	Applies the mean algorithm to the base image that you chose in this dialog box.
   Cancel	Disregards any changes that you made in this dialog box and closes the dialog box.
   Help	Displays online help for this dialog box.