Cost functions used in MIPAV algorithms and Generating graphs: Difference between pages

From MIPAV
(Difference between pages)
Jump to navigation Jump to search
m (1 revision imported)
 
MIPAV>Angelfish100
 
Line 1: Line 1:
A similarity or cost function measures the similarity between two images. During the registration the adjusted image V is transformed using the various transformation functions. And the similarity S(U;Vt) between the reference image U and transformed image Vt is then calculated.
MIPAV allows you to generate intensity profiles, or contour VOI graphs, for VOI contours. For delineated VOIs, you can generate 2D, 3D, or 4D intensity graphs. You can also generate a 3D intensity graph at a specific point across all slices in a dataset. For information on how to contour a VOI, refer to Chapter 1, "Segmenting Images Using Contours and Masks,"<br />


'''Note:''' in MIPAV, we use the term cost function to refer to the negative cost function. That means that we assume that the transformation that gives the smallest value of the chosen inverse cost function is the transformation that also gives the best alignment.
=== Generating contour VOI graphs ===
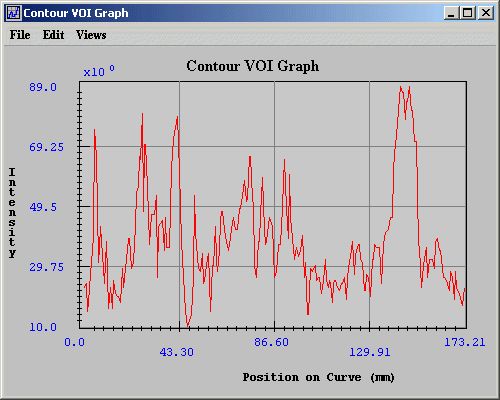
Contour VOI graphs display the intensity values of the selected contour's boundary in the Contour VOI Graph window (Figure 10). You can generate either 2D or 3D contour VOI graphs. <br />


== Background ==
'''To generate 2D contour VOI graphs'''<br />
[[File:CostFunctions1.jpg |200px|thumb|right|The plots of the Correlation Ratio cost function versus some of the individual parameter values. In each plot (A, B, C, and D), a single parameter is varied while the other are kept constant]]
1 Open an image.<br />
2 Delineate a 2D VOI on the image using one of the 2D icons in the MIPAV window.<br />


For the registration algorithms, such as [[Optimized automatic registration 3D | OAR]], the main approach for determining an optimal transformation is to


<ol>
{| border="1" cellpadding="5"
    <li>Calculate a cost function,</li>
|+ '''Figure 10. Contour VOI Graph window '''
    <li>Determine how it changes as individual transformation parameters are varied,</li>
|-
    <li>And find the parameters that minimize the value of the cost function.</li>
| rowspan="1" colspan="3" |
</ol>
[[Image:windowContourVOIGraph.jpg]]
|-
| rowspan="4" colspan="1" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">File</font>'''</span></div>
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Open Graph</font>'''</span>-Opens a PLT file that contains graph data. When you select this command or press Ctrl O on the keyboard, the Open Graph Data dialog box appears. </div>
|-
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Save Graph</font>'''</span>-Saves the graph data in a PLT file. When you select this command or when you press Ctrl S on the keyboard, the Save dialog box opens.</div>
|-
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Print Graph</font>'''</span>-Allows you to print the graph. When you select this command or press <br />Ctrl P, the Print dialog box opens.</div>
|-
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Close Graph</font>'''</span>-Closes the Intensity Graph window. To close the window, you can also press Ctrl X on the keyboard.</div>
|-
| rowspan="3" colspan="1" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Edit</font>'''</span></div>
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Delete Function</font>'''</span>-Allows you to delete a specific function. However, you cannot delete a function if it is the only function displayed in the window.</div>
|-
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Copy Function</font>'''</span>-Copies a function that is currently displayed in the window.</div>
|-
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Paste Function</font>'''</span>-Pastes a previously copied function into the window. The pasted function has a different color than the first function displayed in the window.</div>
|-
| rowspan="3" colspan="1" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Views</font>'''</span></div>
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Modify Graph Features</font>'''</span>-Allows you to customize the appearance of the graph.</div>
|-
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Reset Range to Default</font>'''</span>-<span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">[TBD]</font>'''</span></div>
|-
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Reset Graph to Original</font>'''</span>-<span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">[TBD]</font>'''</span>. </div>
|-
|
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Help</font>'''</span></div>
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Help Topics</font>'''</span>-Displays online help topics.</div>
|}


The following figure (right) shows a plot of a sample cost function for a selection of transformation parameters.
<br />
3 Select the VOI. <br />
As an option, copy the VOI to other slices in the dataset by selecting VOI &gt; Propagate and one of the following commands:<br />
*To Next Slice<br />
*To Previous Slice<br />
*To All Slices<br />
4 Do one of the following:<br />
*Select VOI &gt; Graph &gt; Boundary Intensity in the MIPAV window. <br />
*Right click on the VOI and then select Graph &gt; Boundary Intensity.<br />
*The Contour VOI Graph window (Figure 10) opens.<br />


The cost functions implemented in MIPAV:
'''To generate 3D contour VOI graphs'''<br />
1 Open an image.<br />
2 Delineate a VOI on the image using the 3D rectangular VOI icon, in the MIPAV window. <br />
3 Select the VOI. <br />
As an option, copy the VOI to other slices in the dataset by selecting VOI &gt; Propagate and one of the following commands:<br />
*To Next Slice<br />
*To Previous Slice<br />
*To All Slices<br />
4 Do one of the following:<br />
*Select VOI &gt; Graph &gt; Boundary Intensity in the MIPAV window.<br />
*Right-click on the VOI and then select Graph &gt; Boundary Intensity. <br />
The Contour VOI Graph window (Figure 10) opens. This window displays a graph of the intensity values of the selected contour's boundary. <br />


*[[#CorrelationRatio | Correlation ratio]]
=== Generating intensity graphs ===
*[[#LaplacianZeroCrossing | Laplacian Zero Crossing]]
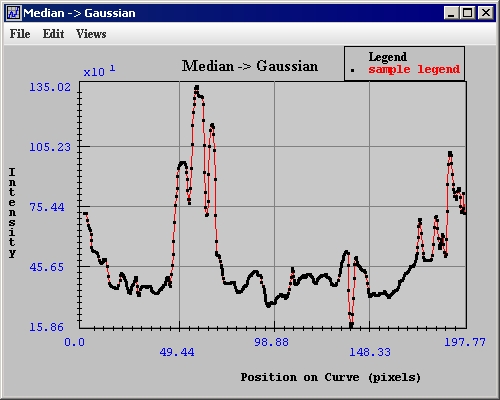
Intensity profiles, or graphs, present information on the intensity values of the VOI region in an image. The intensity graph appears in the Intensity Graph window (Figure 11).<br />
*[[#GradientMagnitude | Gradient Magnitude]]
*[[#LeastSquares | Least Squares]]
*[[#NormalizedCrossCorrelation | Normalized Cross Correlation]]
*[[#NormalizedMutualInformation | Normalized Mutual Information]]


== Powell algorithm ==
'''To generate 2D intensity graphs'''<br />
1 Open an image.<br />
2 Delineate a 2D VOI on the image using one of the 2D icons in the MIPAV window.<br /><
3 Select the VOI. <br />
As an option, copy the VOI to other slices in the dataset by selecting VOI &gt; Propagate and one of the following commands:<br />
*To Next Slice<br />
*To Previous Slice<br />
*To All Slices<br />
4 Do one of the following:<br />
Select VOI &gt; Graph in the MIPAV window and either of the following:<br />
* ''2.5D Total Intensity'' -To generate a graph of the sum of the intensity values of the VOI region. <br />
* ''2.5D Average Intensity'' -To generate a graph of the average of the intensity values of the VOI region.<br />
Right-click on the VOI and then select Graph and one of the following commands:<br />
* ''2.5D Total Intensity'' -To generate a graph of the sum of the intensity values of the area delineated by the VOI per slice.<br />
* ''2.5D Average Intensity'' -To generate a graph of the average of the intensity values of the VOI region.<br />
* ''2.5D Total Intensity with Threshold'' -TBD. <br />
* ''2.5D Average Intensity with Threshold'' -TBD.<br />
The Intensity Graph window (Figure 11) opens.


In MIPAV, most of the methods and algorithms use [http://math.fullerton.edu/mathews/n2003/PowellMethodMod.htm the Powell algorithm] to find the global minimum of the chosen cost function. For more information about the Powell algorithm, refer to [http://math.fullerton.edu/mathews/n2003/PowellMethodMod.htm http://math.fullerton.edu/mathews/n2003/PowellMethodMod.htm].
{| border="1" cellpadding="5"
|+ '''Figure 11. Intensity Graph window '''
|-
|
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">File</font>'''</span></div>
|
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Open Graph</font>'''</span>-Opens a PLT file that contains graph data.</div> <div class="CellBody">When you select this command or press Ctrl O on the keyboard, the Open Graph Data dialog box appears. </div>
| rowspan="2" colspan="1" |
[[Image:VOIGRaphMOdifyPointsVis.jpg]]
|-
|
<div class="CellBody"> </div>
|
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Save Graph</font>'''</span>-Saves the graph data in a PLT file. </div> <div class="CellBody">When you select this command or when you press Ctrl S on the keyboard, the Save dialog box opens.</div>
|-
|
<div class="CellBody"> </div>
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Print Graph</font>'''</span>-Allows you to print the graph. When you select this command or press <br />Ctrl P, the Print dialog box opens.</div>
|-
|
<div class="CellBody"> </div>
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Close Graph</font>'''</span>-Closes the Intensity Graph window. To close the window, you can also press Ctrl X on the keyboard.</div>
|-
|
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Edit</font>'''</span></div>
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Delete Function</font>'''</span>-Allows you to delete the function that you select. However, you cannot delete a function if it is the only function displayed in the window.</div>
|-
|
<div class="CellBody"> </div>
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Paste Function</font>'''</span>-Pastes a previously copied function into the window. The pasted function has a different color than the first function displayed in the window.</div>
|-
|
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Views</font>'''</span></div>
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Modify Graph Features</font>'''</span>-Allows you to customize the appearance of the graph.</div>
|-
|
<div class="CellBody"> </div>
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Reset Range to Default</font>'''</span>-TBD.</div>
|-
|
<div class="CellBody"> </div>
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Reset Graph to Original</font>'''</span>-TBD.</div>
|-
|
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Help</font>'''</span></div>
| rowspan="1" colspan="2" |
<div class="CellBody"><span style="font-style: normal; text-decoration: none; text-transform: none; vertical-align: baseline">'''<font color="#000000">Help Topics</font>'''</span>-Displays online help topics.</div>
|}


<div id="CorrelationRatio"></div>
'''To generate 3D intensity graphs of all slices in a dataset at a specific point'''<br />
== Correlation Ratio ==
1 Open an image.<br />
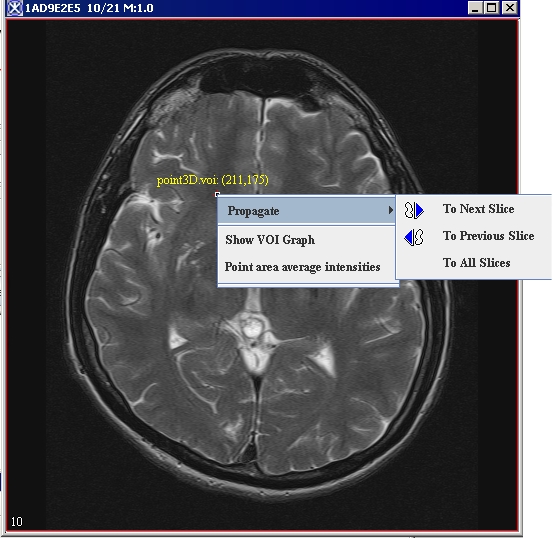
2 Draw a point VOI on the image (Figure 12).<br />
3 Select the VOI.<br />
4 Do one of the following:<br />
*Select the Propagate VOI to all slices icon.<br />
*Select VOI &gt; Propagate &gt; To All Slices. <br />
*Right-click on the VOI, then select Propagate &gt; To All Slices (Figure 12).<br />
5 Right-click on the VOI and select Show VOI Graph (Figure 12).<br />


Given two images I and R, the basic principle of the Correlation Ratio method is to search for a spatial transformation T and an intensity mapping f such that, by displacing R and remapping its intensities, the resulting image f(R* T) be as similar as possible to I. This could be achieved by minimizing the following correlation ratio function:  
{| border="1" cellpadding="5"
|+ '''Figure 12. Point VOI'''
|-
|
<div style="font-style: normal; font-weight: normal; margin-bottom: 0pt; margin-left: 0pt; margin-right: 0pt; margin-top: 0pt; text-align: left; text-decoration: none; text-indent: 0pt; text-transform: none; vertical-align: baseline"><font color="#000000">  <br /></font></div>


<math>
<br clear="all" />
min(T,f) of \displaystyle\sum\limits_{k} {I (x_k)-f(R(T(x_k)))}
</math>


which integrates over the voxel positions <math>x_k</math> in the image I.
{|
|
=== Image types ===
[[Image:PointVOIPropagate.jpg]]
|}


Correlation Ratio can be used in multimodal image registration of Magnetic Resonance (MR), Computed Tomography (CT), and Positron Emission Tomography (PET) images.
'''To generate 3D intensity graphs of specific areas'''<br />
1 Open an image.<br />
2 Delineate a VOI on the image using the 3D rectangular VOI icon.<br />
3 Select the VOI. Then, do one of the following:<br />
*a Select VOI &gt; Graph and either of the following in the MIPAV window:<br />
** ''2.5D Total Intensity'' -To generate a graph of the sum of the intensity values of the area delineated by the VOI per slice.<br />
** ''2.5D Average Intensity'' -To generate a graph of the average of the intensity values of the VOI region.<br />
*b Right-click the VOI, and then select Graph and one of the following commands in the MIPAV window:<br />
** ''2.5D Total Intensity'' -To generate a graph of the sum of the intensity values of the area delineated by the VOI per slice.<br />
** ''2.5D Average Intensity'' -To generate a graph of the average of the intensity values of the VOI region.<br />
** ''2.5D Total Intensity with Threshold'' -TBD.<br />
** ''2.5D Average Intensity with Threshold'' -TBD.<br />
The Intensity Graph window (Figure 11) opens.<br />


<div id="LaplacianZeroCrossing"></div>


== Laplacian Zero-Crossing ==
[[Customizing the appearance of graphs - Modify graph dialog box]]
 
The laplacian zero-crossing is a binary edge feature used for edge detection, see also [[Edge Detection: Zero X Laplacian | Edge Detection: Zero X Laplacian algorithm]]. Convolution of an image with a laplacian kernel approximates the 2-nd partial derivative of the image. The laplacian zero-crossing corresponds to points of maximal (or minimal) gradient magnitude. Thus, laplacian zero-crossings represent "good" edge properties and should, therefore, have a low local cost meaning edge detection. If IL(q) is the laplacian of an image I at pixel q, then,
 
<math>
\begin{cases}
f_Z(q)= 0; if I_L(q) = 0\\
f_Z(q)= 1; if I_L(q)\neq 0
\end{cases}
</math>
 
Though, application of a discrete laplacian kernel to a digital image produces very few zero-valued pixels. Rather, a zero-crossing is represented by two neighboring pixels that change from positive to negative values. Of these two neighboring pixels, the one closest to zero is used to represent the zero-crossing. The resulting feature cost contains single-pixel wide cost "canyons" used for boundary localization.
 
<div id="GradientMagnitude"></div>
== Gradient Magnitude ==
 
Gradient Magnitude provides a direct correlation between the edge strength and local cost. If <math>I_x</math> and <math>I_y</math> represent the partials of an image I in X and Y directions respectively, then the gradient magnitude G is approximated with the following formula:
 
<math>
G=\sqrt{I^2_x + I^2_y}
</math>
 
The gradient is then scaled and inverted, so high gradients produce low costs and vice-versa. Thus, the gradient component function is
 
<math>
f_G =  \frac{max(G)-G}{max(G)} =1 - \frac{G}{max(G)}
</math>
 
Finally, gradient magnitude costs can be scaled by Euclidean distance. To keep the resulting maximum gradient at unity, <math>f_G(q)</math> can be scaled by 1, if q is a diagonal neighbor to p and by <math>\frac {1}{\sqrt{2}}</math>, if q is a horizontal or vertical neighbor.
 
<div id="LeastSquares"></div>
== Least Squares ==
 
Least squares measures the average of the squared difference in image intensities.
 
<math>
\frac{\sum_{i=1}^{N}\{R(p_i) - I(p_i)\}^2}{N}
</math>
 
Where,
*R(p_i) = reference image(p_i) - minimum reference image value
*I(p_i) = input image(p_i) - minimum input image value
*N = the number of values over which the sum is performed
 
It can be divided by count to normalize the cost function or make it invariant to the number of voxels in the region of overlap. If two images show large differences in image intensity, then we recommend using Scaled Least Squares with a global scaling term added:
 
<math>
\frac{\sum_{i=1}^{N}\{R(p_i) - s*I(p_i)\}^2}{N}
</math>
 
=== Image types ===
 
It can be shown that Least Squares is the optimum cost function when two images only differ by Gaussian noise. Images in two different modalities, such as PET and MRI, will never differ by only Gaussian noise. Even two images in the same modality, such as two PET images, will seldom only differ by Gaussian noise as medical scan noise is frequently not Gaussian and because the object often changes between the image acquisitions. The effectiveness of this cost function will be greatly diminished by small numbers of voxels having large intensity differences.
 
<div id="NormalizedCrossCorrelation"></div>
 
== Normalized Cross Correlation ==
 
The Cross-Correlation function can be defined as
 
<math>
CrossCorr(s,t) = \sum_{x}\sum_{y}R(x,y)I(x-s, y-t)
</math>
 
Where,
*R-reference image intensity
*I-input image intensity
 
The summation is taken over the region (s,t) where R and I overlap. For any value of (s,t) inside R(x,y) the cross-correlation function yields one value of CrossCorr. The maximum value of CrossCorr(s,t) indicates the position where I(x,y) best matches R(x,y).
 
Normalized Cross Correlation is 0 for identical images and approaches 1 for images that are very different.
 
=== Image types ===
 
The Cross-Correlation function can be used for aligning the images that have a linear relationship between the intensity values in the images. E.g. images acquired using the same modality. However, the Normalized Cross-Correlation may not work very well in two images that are identical except for a global scaling factor.
 
<div id="NormalizedMutualInformation"></div>
 
== Normalized Mutual Information ==
 
Mutual information (MI) measures how well one image explains the other. In medical image processing, MI is often used as
*a similarity measure for image registration for images that were acquired at different times or by different modalities and
*for combining multiple images to build 3D models.
 
The mutual information  of random variables A and B is defined as:
 
<math>
MI(A,B) = \sum_{ab}p(a,b) log \frac{p(a,b)}{p(a) p(b)}
</math>
 
Where, p(a,b) is the joint probability distribution function of A and B, and p(a) and p(b) are the marginal probability distribution functions of A and B respectively.
 
MI could also be defined as MI(A,B) = H(A) + H(B)-H(A,B),
 
Where H(A) and H(B) are the [http://www.pandasthumb.org/archives/2004/05/shannon-entropy.html Shannon entropy] of image A and B respectively, computed  based on the probability distributions of their grey values. And H(A,B) denotes the conditional entropy, which is based on the conditional probabilities p(a |b) - the chance of grey value a in image A given that the corresponding voxel in B has grey value b. MI measures the distance between the joint distributions of the images' gray values p(a,b) and the distribution when assume that images are independent from each other.
 
=== Normalized mutual information ===
Normalized mutual information can be calculated as normalized MI, where
<math>NMI(A,B) = (H(A) + H(B))/H(A,B)</math>.
 
=== Image types ===
 
The normalized mutual information has been shown to work very well for registering multi-modality images and also time series images. In MIPAV the normalized mutual information approaches 0 for identical images and approaches 1 for images that are very different.
 
== References ==
 
Bjorn Hamre "Three-dimensional image registration of magnetic resonance (MRI) head volumes" Section for Medical Image Analysis and Informatics Department of Physiology & Department of Informatics University of Bergen, Norway.
 
Woods R.P., Handbook of Medical Image Processing and Analysis, Chapter 33 "Within-Modality Registration Using Intensity-Based Cost Functions", Editor, Isaac N. Bankman, Academic Press, 2000, pp. 529-553.
 
Mortensen E., Barrett W., "Intelligent scissors for image composition", International Conference on Computer Graphics and Interactive Techniques archive. Proceedings of the 22-nd annual conference on Computer graphics and interactive techniques, pp. 191 - 198, 1995, ISBN:0-89791-701-4.
 
Josien P. W. Pluim, J. B. Antoine Maintz and Max A. Viergever. Mutual information based registration of medical images: a survey. IEEE TRANSACTIONS ON MEDICAL IMAGING, VOL. XX, NO. Y, MONTH 2003.
 
Powell method to find the global minimum: [http://math.fullerton.edu/ mathews/n2003/PowellMethodMod.html http://math.fullerton.edu/ mathews/n2003/PowellMethodMod.html]
 
== See also ==
*[http://mipav.cit.nih.gov/wiki/index.php/Main_Page MIPAV WIKI]
*[[Using MIPAV Algorithms]]
*[[Degrees of freedom]]
 
[[Category:Help]]
[[Category:Help:Algorithms]]

Revision as of 20:22, 21 February 2012

MIPAV allows you to generate intensity profiles, or contour VOI graphs, for VOI contours. For delineated VOIs, you can generate 2D, 3D, or 4D intensity graphs. You can also generate a 3D intensity graph at a specific point across all slices in a dataset. For information on how to contour a VOI, refer to Chapter 1, "Segmenting Images Using Contours and Masks,"

Generating contour VOI graphs

Contour VOI graphs display the intensity values of the selected contour's boundary in the Contour VOI Graph window (Figure 10). You can generate either 2D or 3D contour VOI graphs.

To generate 2D contour VOI graphs
1 Open an image.
2 Delineate a 2D VOI on the image using one of the 2D icons in the MIPAV window.


Figure 10. Contour VOI Graph window

WindowContourVOIGraph.jpg

File
Open Graph-Opens a PLT file that contains graph data. When you select this command or press Ctrl O on the keyboard, the Open Graph Data dialog box appears.
Save Graph-Saves the graph data in a PLT file. When you select this command or when you press Ctrl S on the keyboard, the Save dialog box opens.
Print Graph-Allows you to print the graph. When you select this command or press
Ctrl P, the Print dialog box opens.
Close Graph-Closes the Intensity Graph window. To close the window, you can also press Ctrl X on the keyboard.
Edit
Delete Function-Allows you to delete a specific function. However, you cannot delete a function if it is the only function displayed in the window.
Copy Function-Copies a function that is currently displayed in the window.
Paste Function-Pastes a previously copied function into the window. The pasted function has a different color than the first function displayed in the window.
Views
Modify Graph Features-Allows you to customize the appearance of the graph.
Reset Range to Default-[TBD]
Reset Graph to Original-[TBD].
Help
Help Topics-Displays online help topics.


3 Select the VOI.
As an option, copy the VOI to other slices in the dataset by selecting VOI > Propagate and one of the following commands:

  • To Next Slice
  • To Previous Slice
  • To All Slices

4 Do one of the following:

  • Select VOI > Graph > Boundary Intensity in the MIPAV window.
  • Right click on the VOI and then select Graph > Boundary Intensity.
  • The Contour VOI Graph window (Figure 10) opens.

To generate 3D contour VOI graphs
1 Open an image.
2 Delineate a VOI on the image using the 3D rectangular VOI icon, in the MIPAV window.
3 Select the VOI.
As an option, copy the VOI to other slices in the dataset by selecting VOI > Propagate and one of the following commands:

  • To Next Slice
  • To Previous Slice
  • To All Slices

4 Do one of the following:

  • Select VOI > Graph > Boundary Intensity in the MIPAV window.
  • Right-click on the VOI and then select Graph > Boundary Intensity.

The Contour VOI Graph window (Figure 10) opens. This window displays a graph of the intensity values of the selected contour's boundary.

Generating intensity graphs

Intensity profiles, or graphs, present information on the intensity values of the VOI region in an image. The intensity graph appears in the Intensity Graph window (Figure 11).

To generate 2D intensity graphs
1 Open an image.
2 Delineate a 2D VOI on the image using one of the 2D icons in the MIPAV window.
< 3 Select the VOI.
As an option, copy the VOI to other slices in the dataset by selecting VOI > Propagate and one of the following commands:

  • To Next Slice
  • To Previous Slice
  • To All Slices

4 Do one of the following:
Select VOI > Graph in the MIPAV window and either of the following:

  • 2.5D Total Intensity -To generate a graph of the sum of the intensity values of the VOI region.
  • 2.5D Average Intensity -To generate a graph of the average of the intensity values of the VOI region.

Right-click on the VOI and then select Graph and one of the following commands:

  • 2.5D Total Intensity -To generate a graph of the sum of the intensity values of the area delineated by the VOI per slice.
  • 2.5D Average Intensity -To generate a graph of the average of the intensity values of the VOI region.
  • 2.5D Total Intensity with Threshold -TBD.
  • 2.5D Average Intensity with Threshold -TBD.

The Intensity Graph window (Figure 11) opens.

Figure 11. Intensity Graph window
File
Open Graph-Opens a PLT file that contains graph data.
When you select this command or press Ctrl O on the keyboard, the Open Graph Data dialog box appears.

VOIGRaphMOdifyPointsVis.jpg

Save Graph-Saves the graph data in a PLT file.
When you select this command or when you press Ctrl S on the keyboard, the Save dialog box opens.
Print Graph-Allows you to print the graph. When you select this command or press
Ctrl P, the Print dialog box opens.
Close Graph-Closes the Intensity Graph window. To close the window, you can also press Ctrl X on the keyboard.
Edit
Delete Function-Allows you to delete the function that you select. However, you cannot delete a function if it is the only function displayed in the window.
Paste Function-Pastes a previously copied function into the window. The pasted function has a different color than the first function displayed in the window.
Views
Modify Graph Features-Allows you to customize the appearance of the graph.
Reset Range to Default-TBD.
Reset Graph to Original-TBD.
Help
Help Topics-Displays online help topics.

To generate 3D intensity graphs of all slices in a dataset at a specific point
1 Open an image.
2 Draw a point VOI on the image (Figure 12).
3 Select the VOI.
4 Do one of the following:

  • Select the Propagate VOI to all slices icon.
  • Select VOI > Propagate > To All Slices.
  • Right-click on the VOI, then select Propagate > To All Slices (Figure 12).

5 Right-click on the VOI and select Show VOI Graph (Figure 12).

Figure 12. Point VOI


PointVOIPropagate.jpg

To generate 3D intensity graphs of specific areas
1 Open an image.
2 Delineate a VOI on the image using the 3D rectangular VOI icon.
3 Select the VOI. Then, do one of the following:

  • a Select VOI > Graph and either of the following in the MIPAV window:
    • 2.5D Total Intensity -To generate a graph of the sum of the intensity values of the area delineated by the VOI per slice.
    • 2.5D Average Intensity -To generate a graph of the average of the intensity values of the VOI region.
  • b Right-click the VOI, and then select Graph and one of the following commands in the MIPAV window:
    • 2.5D Total Intensity -To generate a graph of the sum of the intensity values of the area delineated by the VOI per slice.
    • 2.5D Average Intensity -To generate a graph of the average of the intensity values of the VOI region.
    • 2.5D Total Intensity with Threshold -TBD.
    • 2.5D Average Intensity with Threshold -TBD.

The Intensity Graph window (Figure 11) opens.


Customizing the appearance of graphs - Modify graph dialog box

Retrieved from "https://mipav.cit.nih.gov/pubwiki/index.php?title=Cost_functions_used_in_MIPAV_algorithms&oldid=229"