Filters (Spatial): Median and Filters (Spatial): Mode: Difference between pages

From MIPAV
(Difference between pages)
Jump to navigation Jump to search
m (1 revision imported)
 
MIPAV>Olgavovk
mNo edit summary
 
Line 1: Line 1:
== Background ==
Mode filtering is a nonlinear spatial filtering technique that replaces a target pixel with the mode of neighboring pixels. The ''mode'' of a set of values is the value that occurs most frequently within the set. If all values are unique-that is, all numbers occur only once in the set-the value of the target pixel stays the same. Mode filtering is similar in philosophy to median filtering.
The Median filter algorithm replaces a target pixel's value with the median value of the neighboring pixels. The designation of ''neighbor'' is determined by the size and shape of the kernel. A kernel is much like a mask; the pixels in the masked area are part of the neighborhood. The kernel's size and shape determines the number of pixel values used to calculate the median. You can adjust this algorithm's parameters to change the kernel's size and shape, apply selective filtering, and repetitively apply the selected filtering for any portion of the image you select.


The median filter algorithm is most useful for removing ''shot noise'', which is noise that appears as random spots in an image. Shot noise can be caused by dust or a bad detector in image acquisition or by errors in data transfer (Lyon, Russ). Note that because there is no inverse function for the median filter algorithm, the original image cannot be reconstructed. This algorithm is also called a ''rank-type filter,'' because the list of values must be sorted before a useful value can be found.
Mode filtering is currently thought to be useful in filtering a segmented image to eliminate small clusters of pixels labeled one value that are completely within a large cluster of pixels of a different value. Mode filtering is currently being investigated in improving a C-means classification of brain images, which were first segmented using the brain extraction tool (BET). Mode filtering can be applied to grayscale images to remove some noise; however, a 3 x 3 x 3 cube kernel significantly blurs the image.


{| width="90%" border="1" frame="hsides" frame="hsides"
=== Background ===
 
When you apply the Mode algorithm, MIPAV identifies the target pixel and collects the values of the surrounding neighborhood. Next, it arranges the values of the target and neighborhood pixels in a list and sorts them. The value of the target pixel is replaced with the mode of the numbers in the list. Determining the mode of a sorted list of numbers is done in a single pass through the list by incrementing a count variable each time adjacent values are the same and maintaining the maximum count along with the corresponding value.
 
Neighborhood pixels are determined by the shape and size of the kernel. (The selection of pixels using the kernel is sometimes referred to as the ''sliding window approach''.) The most common kernel shapes are the square and cross.
 
Square-shaped kernels are defined as all pixels in the ''k''(''k'') region surrounding the target pixel, where k refers to the window size. Cross-shaped kernels are defined as the central row and column of the ''k''(''k'') region.
 
The kernel is usually centered on the target pixel and is symmetrical; pixels chosen are symmetrically located about the target pixel. Thus, pixels on opposite sides are equally weighted. The kernel varies in size, although commonly a square kernel can range from 3 to 11 pixels per side. Other kernel shapes and sizes could be selected, but choosing the region of pixels to include always involves juggling the elimination of noise and increasing fuzziness and posterization of an image.
 
Pixel values are sorted in increasing order. Any sorting method is acceptable, although, because the number of pixels can be large, a fast- sorting algorithms is preferable. The best sorting algorithm is one that can efficiently accommodate both small and large lists. Generally, when considering the number of items to sort, the numbers can range from 5 (in a 3 x 3 cross) to 121 (in an 11 x 11 square). This algorithm implements the Shell-sort because it operates very efficiently for the sizes of the lists expected.
 
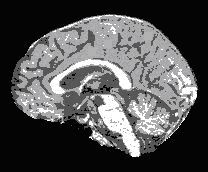
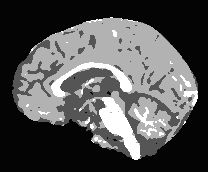
The left image in Figure 1 shows a segmented image that results after applying the C-means classification algorithm to a brain image produced with the brain extraction tool. The image on the right shows the result of applying the Mode filtering algorithm with a 3 x 3 x 3 local neighborhood to the image on the left. Clearly, the image on the right has fewer small isolated classes than the image on the left.
 
<div>
 
{| border="1" cellpadding="5"
|+ <div>'''Figure 1. Examples of (A) a segmented image and (B) the results of applying the Mode algorithm to the image''' </div>
|-
|-
| width="9%" valign="top" |
|
[[Image:noteicon.gif]]
<div><div><center>[[Image:exampleMode1.jpg]]</center></div> </div>
| width="81%" bgcolor="#B0E0E6" |
|
[http://mipav.cit.nih.gov/ For more information about the algorithm, refer to MIPAV Volume 2 User Guide on the MIPAV web site:{http://mipav.cit.nih.gov/} ]
<div><div><center>[[Image:exampleMode2.jpg]]</center></div> </div>
|}
|}


<br />
</div>


== Image types ==
The Mode algorithm processes all pixels in the input image. The algorithm uses a symmetric neighborhood definition around the target pixel, resulting in border pixels, which require special processing. Border pixels correspond to those pixels where the neighborhood of a target pixel is incomplete. Incomplete neighborhoods occur:


You can apply this algorithm to color and gray-scale 2D, 2.5D, and 3D images. However, you cannot apply this algorithm to complex images.
* ''In-plane''-In the corners of the image plane
* ''Through-plane''-On the first and last (few) image planes


<div> </div>
In-plane border pixels are not filtered and the value assigned to the output pixel is simply the corresponding input value. Through-plane border pixels are filtered by duplicating the values of corresponding pixels on the target pixel plane.


== Special notes ==
==== Image types ====


The following special notes apply:
You can apply this algorithm to 2D, 2.5D, and 3D images. Since the algorithm counts the number of pixels with the same value, it only allows the following list of data types.


* When this algorithm is applied to 3D datasets, you can apply the filter to either a single slice or volume kernel. If you choose to apply it to a volume kernel, MIPAV finds the median in a list of values from pixels in all directions along the ''x''-, ''y''-, and ''z''-axes. Note that the kernel-size must be smaller than the number of slices in the image.
* BYTE and UBBYTE
* The resultant image is, by default, a float image.
* SHORT and USHORT
* An outlier detector is available for use in this algorithm. The outlier detector replaces the target pixel only if its magnitude exceeds the mean of the list by a user-inputted fraction of the standard deviation.
* INTEGER and UINTEGER
* Currently the algorithm allows square and cross kernel shapes for 2D images and cube and axis kernel shapes for 3D images. Future plans include the addition of other kernel shapes.
* Color images may be filtered across any combination of the color channels (red, green, or blue). Alpha values-those values relating to how opaque a particular pixel is-are unaffected.


<div> </div>
==== Notes ====


== Applying the Median Filter algorithm ==
The resulting image is, by default, the same type as the input image.
 
==== References ====
 
This algorithm was developed by members of the MIPAV team. Mode filtering is similar to median filtering, and to our knowledge there is not a significant amount of literature about the topic.
 
=== Applying the Mode algorithm ===


To run this algorithm, complete the following steps:
To run this algorithm, complete the following steps:


# Select Algorithms &gt; Filter &gt; Median Filter. The Median Filter dialog box appears.
# Open an image.
# Complete the fields in the dialog box. Keep the following in mind:
# Select Algorithms &gt; Filters (Spatial) &gt; Mode. The Mode Filter dialog box ([FiltersSpatialMode.html#wp1006320 Figure 35]) opens.
#* To filter a VOI region only, select the VOI and then select VOI Region(s).
# Complete the fields in the dialog box.
#* Pixels that are too close to the edge of an image are not processed.
#* To apply a median filter to a color image, select the channels to filter. By default, MIPAV filters all three channels (red, green, and blue).
# Click OK when complete. The algorithm begins to run.
# Click OK when complete. The algorithm begins to run.


; A pop-up window appears with the status, and the following message appears: "Filtering Image (Pass 1 of 1)." (Depending on what you entered in Number of iterations on the Median Filter dialog box, the number of passes varies.) When the algorithm finishes running, the pop-up window closes.
; A pop-up window appears with the status.
; Depending on whether New image or Replace image was selected, results appear in a new window or replace the image to which the algorithm was applied.


<div>
<div>


{| border="1" cellpadding="5"
{| border="1" cellpadding="5"
|+ <div>'''Figure 1. Median Filter dialog box  ''' </div>
|+
|-
|-
|
|
<div>'''Number of iterations''' </div>
<div><div><center>[[Image:messageModeFiltering.jpg]]</center></div> </div>
|
|}
<div>Indicates the number of times to filter the image with a median filter of the selected deviation, kernel size, and kernel shape. </div>
 
| rowspan="3" colspan="1" |
</div>
<div> </div><div><div><center>[[Image:MedianFilterdialogBox.jpg]]</center></div> </div>
 
|-
; When the algorithm finishes running, the pop-up window closes.
|
; Depending on whether New image or Replace image was selected, results appear in a new window or replace the image to which the algorithm was applied.
<div>'''Maximum standard deviation''' </div>
 
|
<div>
<div>The maximum allowable magnitude of the pixel value as a function of the standard deviation. The system replaces any pixel whose value is outside this function of the standard deviation from the mean of the neighborhood (as selected by the kernel-size and shape) by the median of the neighborhood. A value of 0.0 is equivalent to replacing every pixel with the median of its neighborhood. A value of 1.0 limits the filtering of the image. The system processes only target pixels whose values are greater than 1.0 standard deviation from its neighbors. </div>
 
{| border="1" cellpadding="5"
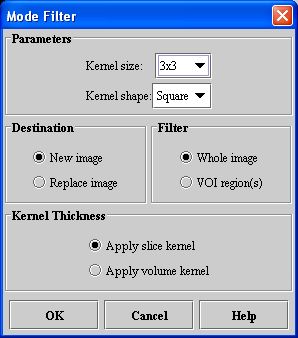
|+ <div>'''Figure 2. Mode Filter dialog box ''' </div>
|-
|-
|
|
<div>'''Kernel size''' </div>
<div>'''Kernel size''' </div>
|
|
<div>A ''k'''' x ''''k'' region selects a neighborhood that extends in all directions by ''(''''k''''-1)/2'', placing the target pixel in the center of the kernel. </div>
<div>Specifies the size of the local neighborhood when performing mode filtering. A ''k'' x ''k'' region selects a neighborhood that extends in all directions by (''k'' - 1)/2 placing the target pixel in the center of the kernel. Kernels for 2D images are odd valued and include 3 x 3, 5 x 5, 7 x 7, and so on. </div>
| rowspan="4" colspan="1" |
<div><div><center>[[Image:dialogboxModeFilter.jpg]]</center></div> </div>
|-
|-
|
|
<div>'''Kernel shape''' </div>
<div>'''Kernel shape''' </div>
| rowspan="1" colspan="2" |
<div>Selects which pixels in the kernel size box are included as a part of the median's neighborhood. </div>
|-
|
<div>Kernel size adaptively changes </div>
| rowspan="1" colspan="2" |
<div>This checkbox indicates whether median filter should be run via adaptive filtering. Adaptive filtering has 3 main purposes:  </div><div>1. To remove salt-and-pepper (impulse) noise;  </div><div>2. To prove smoothing of other noise that may not be impulsive; </div><div>3. And to reduce distortion, such as excessive thinning or thickening of object borders. </div>
|-
|
|
<div>Maximum Kernel Size </div>
<div>Selects which pixels in the kernel size box are included as a part of the mode's neighborhood. </div>
| rowspan="1" colspan="2" |
<div> This is the maximum kernel size that the window size can get increased to under the algorithm. </div>
|-
|-
|
|
<div>'''Red channel''' </div>
<div>'''New image''' </div>
| rowspan="1" colspan="2" |
<div>Filters the red channel (for use with RGB images). </div>
|-
|
<div>'''Green channel''' </div>
| rowspan="1" colspan="2" |
<div>Filters the green channel (for use with RGB images). </div>
|-
|
<div>'''Blue channel''' </div>
| rowspan="1" colspan="2" |
<div>Filters the blue change (for use with RGB images). </div>
|-
|
|
<div>'''New image''' </div>
| rowspan="1" colspan="2" |
<div>Indicates where the results of the algorithm appear. If you select this option, the results appear in a new image window. </div>
<div>Indicates where the results of the algorithm appear. If you select this option, the results appear in a new image window. </div>
|-
|-
|
|
<div>'''Replace image''' </div>
<div>'''Replace image''' </div>
| rowspan="1" colspan="2" |
|
<div>Indicates where the results of the algorithm appear. If you select this option, the results replace the current active image. </div>
<div>Indicates where the results of the algorithm appear. If you select this option, the results replace the current active image. </div>
|-
|-
|
|
Line 121: Line 118:
<div>'''Apply slice kernel''' </div>
<div>'''Apply slice kernel''' </div>
| rowspan="1" colspan="2" |
| rowspan="1" colspan="2" |
<div>Filters each slice of the image independently of other slices, finding neighboring pixels from the slice. </div>
<div>Filters each slice of the image independently of other slices, finding neighboring pixels from the slice. </div>
|-
|-
|
|
<div>'''Apply volume kernel ''' </div>
<div>'''Apply volume kernel''' </div>
| rowspan="1" colspan="2" |
| rowspan="1" colspan="2" |
<div>Gathers pixel values from the slice as well as from neighboring slices. </div>
<div>Gathers pixel values from the slice as well as from neighboring slices. </div>
|-
|-
|
|
<div>'''OK''' </div>
<div>'''OK''' </div>
| rowspan="1" colspan="2" |
| rowspan="1" colspan="2" |
<div>Applies the Median algorithm according to the specifications in this dialog box. </div>
<div>Applies the Mode filtering algorithm according to the specifications in this dialog box. </div>
|-
|-
|
|
Line 143: Line 140:
<div>Displays online help for this dialog box. </div>
<div>Displays online help for this dialog box. </div>
|}
|}
== See also: ==
**[[Filters (Spatial): Adaptive Path Smooth]]
**[[Filters (Spatial) Anisotropic Diffusion]]
**[[Filters (Spatial): Coherence-Enhancing Diffusion]]
**[[Filters (Spatial): Gaussian Blur]]
**[[Filters (Spatial): Gradient Magnitude]]
**[[Filters (Spatial): Haralick Texture]]
**[[Filters (Spatial) Laplacian]]
**[[Filters (Spatial): Local Normalization]]
**[[Filters (Spatial): Mean]]


[[Category:Help]]
[[Category:Help]]
[[Category:Help:Algorithms]]
[[Category:Help:Algorithms]]

Revision as of 18:26, 18 May 2012

Mode filtering is a nonlinear spatial filtering technique that replaces a target pixel with the mode of neighboring pixels. The mode of a set of values is the value that occurs most frequently within the set. If all values are unique-that is, all numbers occur only once in the set-the value of the target pixel stays the same. Mode filtering is similar in philosophy to median filtering.

Mode filtering is currently thought to be useful in filtering a segmented image to eliminate small clusters of pixels labeled one value that are completely within a large cluster of pixels of a different value. Mode filtering is currently being investigated in improving a C-means classification of brain images, which were first segmented using the brain extraction tool (BET). Mode filtering can be applied to grayscale images to remove some noise; however, a 3 x 3 x 3 cube kernel significantly blurs the image.

Background

When you apply the Mode algorithm, MIPAV identifies the target pixel and collects the values of the surrounding neighborhood. Next, it arranges the values of the target and neighborhood pixels in a list and sorts them. The value of the target pixel is replaced with the mode of the numbers in the list. Determining the mode of a sorted list of numbers is done in a single pass through the list by incrementing a count variable each time adjacent values are the same and maintaining the maximum count along with the corresponding value.

Neighborhood pixels are determined by the shape and size of the kernel. (The selection of pixels using the kernel is sometimes referred to as the sliding window approach.) The most common kernel shapes are the square and cross.

Square-shaped kernels are defined as all pixels in the k(k) region surrounding the target pixel, where k refers to the window size. Cross-shaped kernels are defined as the central row and column of the k(k) region.

The kernel is usually centered on the target pixel and is symmetrical; pixels chosen are symmetrically located about the target pixel. Thus, pixels on opposite sides are equally weighted. The kernel varies in size, although commonly a square kernel can range from 3 to 11 pixels per side. Other kernel shapes and sizes could be selected, but choosing the region of pixels to include always involves juggling the elimination of noise and increasing fuzziness and posterization of an image.

Pixel values are sorted in increasing order. Any sorting method is acceptable, although, because the number of pixels can be large, a fast- sorting algorithms is preferable. The best sorting algorithm is one that can efficiently accommodate both small and large lists. Generally, when considering the number of items to sort, the numbers can range from 5 (in a 3 x 3 cross) to 121 (in an 11 x 11 square). This algorithm implements the Shell-sort because it operates very efficiently for the sizes of the lists expected.

The left image in Figure 1 shows a segmented image that results after applying the C-means classification algorithm to a brain image produced with the brain extraction tool. The image on the right shows the result of applying the Mode filtering algorithm with a 3 x 3 x 3 local neighborhood to the image on the left. Clearly, the image on the right has fewer small isolated classes than the image on the left.

Figure 1. Examples of (A) a segmented image and (B) the results of applying the Mode algorithm to the image
ExampleMode1.jpg
ExampleMode2.jpg

The Mode algorithm processes all pixels in the input image. The algorithm uses a symmetric neighborhood definition around the target pixel, resulting in border pixels, which require special processing. Border pixels correspond to those pixels where the neighborhood of a target pixel is incomplete. Incomplete neighborhoods occur:

  • In-plane-In the corners of the image plane
  • Through-plane-On the first and last (few) image planes

In-plane border pixels are not filtered and the value assigned to the output pixel is simply the corresponding input value. Through-plane border pixels are filtered by duplicating the values of corresponding pixels on the target pixel plane.

Image types

You can apply this algorithm to 2D, 2.5D, and 3D images. Since the algorithm counts the number of pixels with the same value, it only allows the following list of data types.

  • BYTE and UBBYTE
  • SHORT and USHORT
  • INTEGER and UINTEGER

Notes

The resulting image is, by default, the same type as the input image.

References

This algorithm was developed by members of the MIPAV team. Mode filtering is similar to median filtering, and to our knowledge there is not a significant amount of literature about the topic.

Applying the Mode algorithm

To run this algorithm, complete the following steps:

  1. Open an image.
  2. Select Algorithms > Filters (Spatial) > Mode. The Mode Filter dialog box ([FiltersSpatialMode.html#wp1006320 Figure 35]) opens.
  3. Complete the fields in the dialog box.
  4. Click OK when complete. The algorithm begins to run.
A pop-up window appears with the status.
MessageModeFiltering.jpg
When the algorithm finishes running, the pop-up window closes.
Depending on whether New image or Replace image was selected, results appear in a new window or replace the image to which the algorithm was applied.
Figure 2. Mode Filter dialog box
Kernel size
Specifies the size of the local neighborhood when performing mode filtering. A k x k region selects a neighborhood that extends in all directions by (k - 1)/2 placing the target pixel in the center of the kernel. Kernels for 2D images are odd valued and include 3 x 3, 5 x 5, 7 x 7, and so on.
DialogboxModeFilter.jpg
Kernel shape
Selects which pixels in the kernel size box are included as a part of the mode's neighborhood.
New image
Indicates where the results of the algorithm appear. If you select this option, the results appear in a new image window.
Replace image
Indicates where the results of the algorithm appear. If you select this option, the results replace the current active image.
Whole image
Applies the algorithm to the whole image.
VOI region(s)
Applies the algorithm to the volumes (regions) delineated by the VOIs.
Apply slice kernel
Filters each slice of the image independently of other slices, finding neighboring pixels from the slice.
Apply volume kernel
Gathers pixel values from the slice as well as from neighboring slices.
OK
Applies the Mode filtering algorithm according to the specifications in this dialog box.
Cancel
Disregards any changes that you made in this dialog box and closes the dialog box.
Help
Displays online help for this dialog box.
Retrieved from "https://mipav.cit.nih.gov/pubwiki/index.php?title=Filters_(Spatial):_Median&oldid=203"